Filter
Contents
6. Filter#
Filter sind spezielle Systeme, die in diesem Abschnitt grundsätzlich als LTI-Systeme angenommen werden (es gibt auch nicht LTI-Filter wie z.B. das Median Filter, diese sind aber nicht-linear). Die Aufgabe von Filtern ist typischerweise bestimmte Frequenzanteile aus dem Signal verändern, also zu verstärken, abzuschwächen oder ganz zu entfernen.
Alle nicht-trivialen LTI-Systeme erzeugen eine Filterwirkung, trotzdem werden nicht alle LTI-Systeme als Filter bezeichnet, wenn das Ziel beim Entwurf nicht die Filterwirkung sondern irgendeine andere Eigenschaft ist. Ein Beipiel sei die Berechnung des gleitenden Mittelwertes eines Signals. Eine solches System ist automatisch auch ein Filter, wird aber trotzdem nicht unbedingt als solches bezeichnet. In vielen Fällen ist die Filterwirkung sogar ein unerwünschter Nebeneffekt.
Ziel dieses Abschnittes ist es, die Grundtypen von Filtern kennen zu lernen. Diese können als nicht-rekursive und rekursive Implementierungen vorliegen. Abschließend werden in einer sehr kompakten Form einige bekannte Entwurfsverfahren für die beiden Realisierungsformen vorgestellt.
6.1. Filtertypen#
Bei der Typisierung von Filtern schauen wir uns zunächst die sogenannten Sperrfilter an. Ihr Entwurfsziel ist, möglichst einen bestimmten Frequenzbereich vollständig aus dem Spektrum zu entfernen. Dabei wird zwischen vier Grundtypen unterschieden:
# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0 18.02.2022
#
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------
import matplotlib
import numpy
import scipy
from scipy import signal
from matplotlib import pyplot
# Script to create an ideal and realistic lowpass
# determine where we're running from and set paths accordingly
try:
if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
prefix = ''
except:
prefix = '../../'
matplotlib.style.use(f'{prefix}sv.mplstyle')
Fs = 8000
fg = 1000 # cutoff frequency
order = 6
x = [0.0]*Fs
x[0] = 1.0
b, a = scipy.signal.butter(N=order, Wn=fg, btype='low', output='ba', fs=Fs)
y = scipy.signal.lfilter(b, a, x)
spectrum = numpy.fft.fft(y)
# dB, max amplitude = 0dB
spectrum_abs = 20*numpy.log10(numpy.abs(spectrum)/numpy.abs(spectrum).max())
freq_vec = numpy.linspace(0, Fs, len(spectrum_abs)) # freq bins, for plotting
fig, ax_spectrum = pyplot.subplots()
# ideal frequency respose of filter
ax_spectrum.step(y=[0, 0, -100, - 100, 0], x=[0, fg, Fs/2, Fs-fg, Fs],
color='r', label="Optimale Entwurfsvorgabe")
# actual realization
ax_spectrum.plot(freq_vec, spectrum_abs, color='b',
label="Mögliche Realisierung")
ax_spectrum.set(xlabel='Frequenz in Hz ', ylabel='Dämpfung in dB',
xlim=[0, Fs/2], ylim=[-105, 5], title=f'Tiefpass {order}.Odnung')
pyplot.legend()
pyplot.show()
# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("DesignTP", fig, display=False)
# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0 18.02.2022
#
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------
import matplotlib
import numpy
import scipy
from scipy import signal
from matplotlib import pyplot
# Script to create an ideal and realistic highpass
# determine where we're running from and set paths accordingly
try:
if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
prefix = ''
except:
prefix = '../../'
matplotlib.style.use(f'{prefix}sv.mplstyle')
Fs = 8000
fg = 1000 # cutoff frequency
order = 6
x = [0.0]*Fs
x[0] = 1.0
b, a = scipy.signal.butter(N=order, Wn=fg, btype='high', output='ba', fs=Fs)
y = scipy.signal.lfilter(b, a, x)
spectrum = numpy.fft.fft(y)
# dB, max amplitude = 0dB
spectrum_abs = 20*numpy.log10(numpy.abs(spectrum)/numpy.abs(spectrum).max())
freq_vec = numpy.linspace(0, Fs, len(spectrum_abs)) # freq bins, for plotting
fig, ax_spectrum = pyplot.subplots()
# ideal frequency respose of filter
ax_spectrum.step(y=[-100, -100, 0, 0, -100], x=[0, fg, Fs/2, Fs-fg, Fs],
color='r', label="Optimale Entwurfsvorgabe")
# actual realization
ax_spectrum.plot(freq_vec, spectrum_abs,
color='b', label="Mögliche Realisierung")
ax_spectrum.set(xlabel='Frequenz in Hz ', ylabel='Dämpfung in dB',
xlim=[0, Fs/2], ylim=[-105, 5], title=f'Hochpass {order}.Odnung')
pyplot.legend()
pyplot.show()
# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("DesignHP", fig, display=False)
# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0 18.02.2022
#
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------
import matplotlib
import numpy
import scipy
from scipy import signal
from matplotlib import pyplot
# Script to create an ideal and realistic bandpass
# determine where we're running from and set paths accordingly
try:
if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
prefix = ''
except:
prefix = '../../'
matplotlib.style.use(f'{prefix}sv.mplstyle')
Fs = 8000
fg = [1000, 3000]# cutoff frequency
order = 6
x = [0.0]*Fs
x[0] = 1.0
b,a = scipy.signal.butter(N=order, Wn=fg, btype='bandpass', output='ba', fs=Fs)
y = scipy.signal.lfilter(b, a, x)
spectrum = numpy.fft.fft(y)
# dB, max amplitude = 0dB
spectrum_abs = 20*numpy.log10(numpy.abs(spectrum)/numpy.abs(spectrum).max())
freq_vec = numpy.linspace(0, Fs, len(spectrum_abs)) # freq bins, for plotting
fig, ax_spectrum = pyplot.subplots()
# ideal frequency respose of filter
ax_spectrum.step(y=[-100, -100, 0, -100, -100, 0, -100],
x=[0, fg[0], fg[1], Fs/2, Fs-fg[1], Fs-fg[0], Fs],
color='r', label="Optimale Entwurfsvorgabe")
# actual realization
ax_spectrum.plot(freq_vec, spectrum_abs,
color='b', label="Mögliche Realisierung")
ax_spectrum.set(xlabel='Frequenz in Hz ', ylabel='Dämpfung in dB',
xlim=[0, Fs/2], ylim=[-105, 5], title=f'Bandpass {order}.Odnung')
pyplot.legend()
pyplot.show()
# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("DesignBP", fig, display=False)
# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0 18.02.2022
#
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------
import matplotlib
import numpy
import scipy
from scipy import signal
from matplotlib import pyplot
# Script to create an ideal and realistic bandstop
# determine where we're running from and set paths accordingly
try:
if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
prefix = ''
except:
prefix = '../../'
matplotlib.style.use(f'{prefix}sv.mplstyle')
Fs = 8000
fg = [1000, 3000]# cutoff frequency
order = 6
x = [0.0]*Fs
x[0] = 1.0
b,a = scipy.signal.butter(N=order, Wn=fg, btype='bandstop', output='ba', fs=Fs)
y = scipy.signal.lfilter(b, a, x)
spectrum = numpy.fft.fft(y)
# dB, max amplitude = 0dB
spectrum_abs = 20*numpy.log10(numpy.abs(spectrum)/numpy.abs(spectrum).max())
freq_vec = numpy.linspace(0, Fs, len(spectrum_abs)) # freq bins, for plotting
fig, ax_spectrum = pyplot.subplots()
# ideal frequency respose of filter
ax_spectrum.step(y=[0, 0, -100, 0, 0, -100, 0],
x=[0, fg[0], fg[1], Fs/2, Fs-fg[1], Fs-fg[0], Fs],
color='r', label="Optimale Entwurfsvorgabe")
# actual realization
ax_spectrum.plot(freq_vec, spectrum_abs,
color='b', label="Mögliche Realisierung")
ax_spectrum.set(xlabel='Frequenz in Hz ', ylabel='Dämpfung in dB',
xlim=[0, Fs/2], ylim=[-105, 5], title=f'Bandsperre {order}.Odnung')
pyplot.legend()
pyplot.show()
# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("DesignBS", fig, display=False)
Tiefpass: Ziel des Tiefpasses ist es alle hohen Frequenzen ab einer zu definierenden Grenzfrequenz \(f_\text{g}\) aus dem Spektrum zu entfernen. In der technischen Umsetzung ist es aber nicht möglich, einen abrupten Übergang zwischen dem sog. Durchlassbereich (tiefe Frequenzen beim Tiefpass) und dem Sperrbereich zu realisieren. Eine praktische Realisierung hat deshalb immer bestimmte Grenz- und Übergangsbereiche.
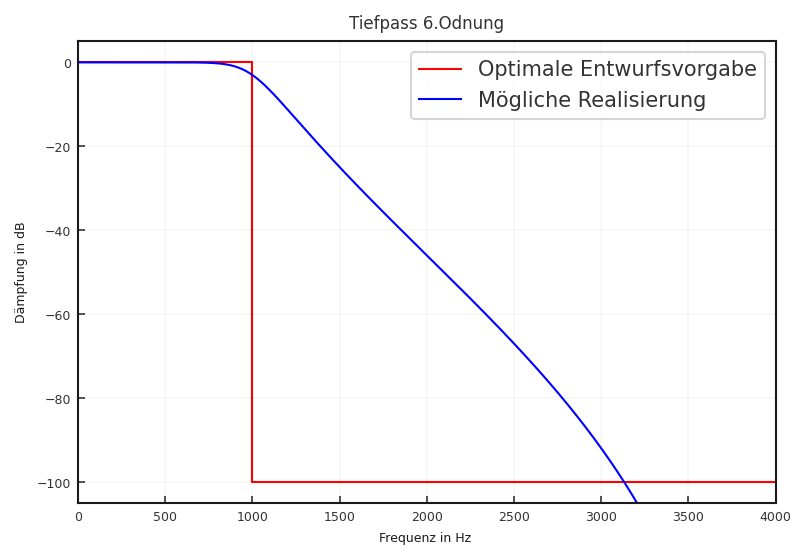
Fig. 6.1 Optimaler Entwurf eines Tiefpasses (\(f_\text{s}\) = 8 kHz und Grenzfrequenz = \(f_\text{g}\) = 1 kHz) und Realisierung durch Butterworth-Filter 6. Ordnung (siehe Abschnitt 6.2.5.1)#
Hochpass: Das inverse Designziel zum Tiefpass liegt dem Hochpassentwurf zu Grunde. Es sollen möglichst alle tiefen Frequenzen aus dem Spektrum entfernt werden. Auch hier gelten die beim Tiefpass erwähnten Einschränkungen.
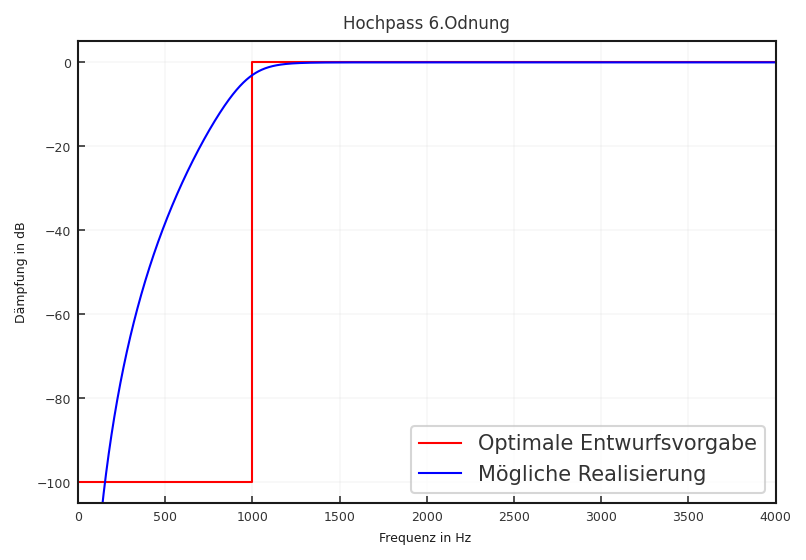
Fig. 6.2 Optimaler Entwurf eines Hochpasses (\(f_\text{s}\) = 8 kHz und Grenzfrequenz = \(f_\text{g}\) = 1 kHz) und Realisierung durch Butterworth-Filter 6. Ordnung (siehe Abschnitt 6.2.5.1)#
Bandpass: Im Gegensatz zu den vorher erwähnten Typen hat das Bandpassfilter zwei Grenzfrequenzen \(f_1\) und \(f_2\). Das Designziel ist, nur die Frequenzen zwischen \(f_1\) und \(f_2\) durchzulassen und alle Frequenzen unterhalb von \(f_1\) bzw. oberhalb von \(f_2\) zu entfernen. Die Differenz zwischen \(f1\) und \(f_2\) wird Bandbreite \(B = f_2 - f_1\) genannt.
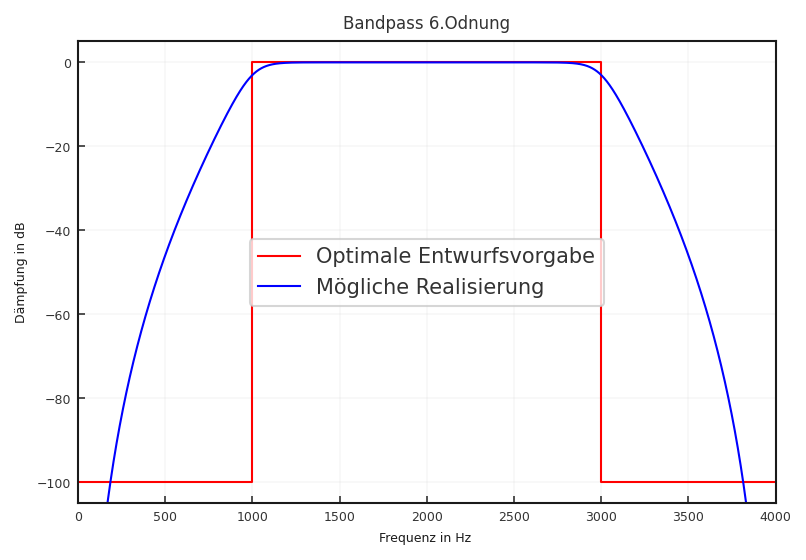
Fig. 6.3 Optimaler Entwurf eines Bandpasses (\(f_\text{s}\) = 8 kHz und Grenzfrequenz \(f_1\) = 1 kHz und \(f_2 =\) 3 kHz) und Realisierung durch Butterworth-Filter 6. Ordnung (siehe Abschnitt 6.2.5.1)#
Bandsperre: Die Bandsperre stellt die inverse Funktion zum Bandpass dar. Bei diesem Entwurf sollen möglichst alle Frequenzen im Bereich zwischen \(f_1\) und \(f_2\) aus dem Spektrum entfernt werden.
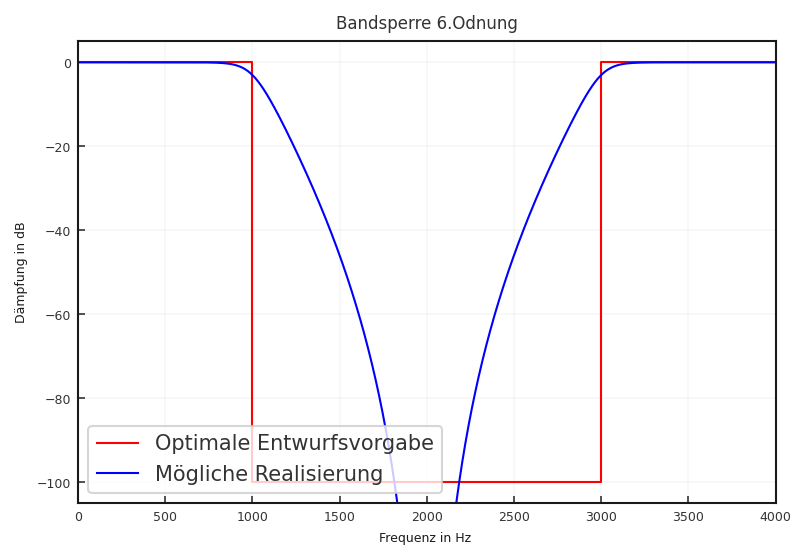
Fig. 6.4 Optimaler Entwurf einer Bandsperre (\(f_\text{s}\) = 8 kHz und Grenzfrequenz \(f_1\) = 1 kHz und \(f_2 =\) 3 kHz) und Realisierung durch Butterworth-Filter 6. Ordnung (siehe Abschnitt 6.2.5.1)#
Eine weitere Gruppe von Filtern hat das Ziel, Signale die durch eine Übertragung verändert wurden, wieder in ihre ursprüngliche Form zurück zu bringen. Das Ziel ist also, ein verändertes Spektrum zu begradigen, bzw. auszugleichen. Aus dieser Aufgabe folgt auch die verwendete englische Typbezeichnung Equalizer. In der Tonstudiotechnik werden diese Filter zwar nicht nur zu diesem Zweck verwendet, aber auch dort werden die Klangformungsfilter als Equalizer bezeichnet. Equalizer ist ein sehr allgemeiner Begriff und kann Filter beinhalten, die eine vollständige Vorgabe der Übertragungsfunktion versuchen zu realisieren. Zum Beispiel bei der Hörgeräteanpassung, die eine vollständige Beschreibung des Hörverlustes als Ausgangsbasis verwendet. Oder aber es werden nur bestimmte Bereiche verändert. Zu dieser letzten Gruppe gehören die Equalizer, wie sie in der Tonstudiotechnik verwendet werden. Hierbei wird zwischen den parametrischen Equalizern und den sogenannten Terzband-Equalizern (eine (große) Terz beschreibt eine drittel Oktave, die wiederum eine Frequenzverdoppelung beschreibt) unterschieden.
Bei den parametrischen Equalizern können durch die drei Parameter
Frequenz,
Verstärkung bzw. Abschwächung und
Güte (\(Q\)-Faktor)
sehr genaue Eingriffe in das Klangspektrum vorgenommen werden. Dabei ist die Güte \(Q = \frac{f_\text{m}}{B}\) als Verhältnis von Mittenfrequenz \(f_\text{m}\) und Bandbreite \(B\) definiert.
# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0 18.02.2022
#
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------
import matplotlib
import numpy
from scipy import signal
from matplotlib import pyplot
from matplotlib.widgets import Slider
# determine where we're running from and set paths accordingly
try:
if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
prefix = ''
except:
prefix = '../../'
matplotlib.style.use(f'{prefix}sv.mplstyle')
def get_peak_EQ(f_0, gain_dB, Q, f_s):
'''
calculates filter coefficients of a peak equalizer
with the given parameters
Parameters:
-----------
f_0 : int
peak frequency in Hz
gain_dB : int
dB gain at peak
Q : float
Quality of filter
f_s : int
sampling frequency
'''
K = numpy.tan(2*numpy.pi*f_0/(f_s*2))
a = [0]*3
b = [0]*3
den = 1
if (gain_dB > 0):
V0 = 10**(gain_dB/20)
den = (1 + K/Q + K*K)
b[0] = (1 + V0*K/Q + K*K)
b[1] = 2 * (K*K - 1)
b[2] = (1 - V0*K/Q + K*K)
a[0] = 1
a[1] = 2 * (K*K - 1)
a[2] = (1 - K/Q + K*K)
else:
V0 = 10**(-gain_dB/20)
den = (1 + V0*K/Q + K*K)
b[0] = (1 + K/Q + K*K)
b[1] = 2 * (K*K - 1)
b[2] = (1 - K/Q + K*K)
a[0] = 1
a[1] = 2 * (K*K - 1)
a[2] = (1 - V0*K/Q + K*K)
b /= den
a[1:] /= den
return b, a
gains = [12, 6, 0, -6, -12]
fs = 48000
freq= 8000
Q = 3
fig, (ax_gain, ax_freq, ax_Q) = pyplot.subplots(3, 1)
for gain in gains:
b, a = get_peak_EQ(freq, gain, Q, fs) # get filter coeefficients
w, h = signal.freqz(b, a, fs) # calculate impulse response
h_db = 20*numpy.log10(numpy.abs(h)) # dB
ax_gain.plot(w, h_db)
ax_gain.set(ylim=[-13, 13], xlabel='Frequenz in Hz', ylabel='Verstärkung in dB',
title=f'Peak-EQ mit variablem Gain \n\
bei Frequenz f = {freq} Hz mit Güte Q = {Q:.1f}')
freqs = [0, fs/10, fs/5, fs/3]
gain = 12
for freq in freqs:
b, a = get_peak_EQ(freq, gain, Q, fs) # get filter coeefficients
w, h = signal.freqz(b, a, fs) # calculate impulse response
h_db = 20*numpy.log10(numpy.abs(h)) # dB
ax_freq.plot(w, h_db)
ax_freq.set(ylim=[-13, 13], xlabel='Frequenz in Hz', ylabel='Verstärkung in dB',
title=f'Peak-EQ mit variabler Frequenz \n\
bei Gain = {gain} dB und Güte Q = {Q:.1f}')
Qs = [0, 1, 3, 10]
freq = 8000
for Q in Qs:
b, a = get_peak_EQ(freq, gain, Q, fs) # get filter coeefficients
w, h = signal.freqz(b, a, fs) # calculate impulse response
h_db = 20*numpy.log10(numpy.abs(h)) # dB
ax_Q.plot(w, h_db)
ax_Q.set(ylim=[-13, 13], xlabel='Frequenz in Hz', ylabel='Verstärkung in dB',
title=f'Peak-EQ mit variabler Güte \n\
bei Frequenz f = {freq} Hz und Gain = {gain} dB')
pyplot.tight_layout()
pyplot.show()
# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("EQ_GainParam", fig, display=False)
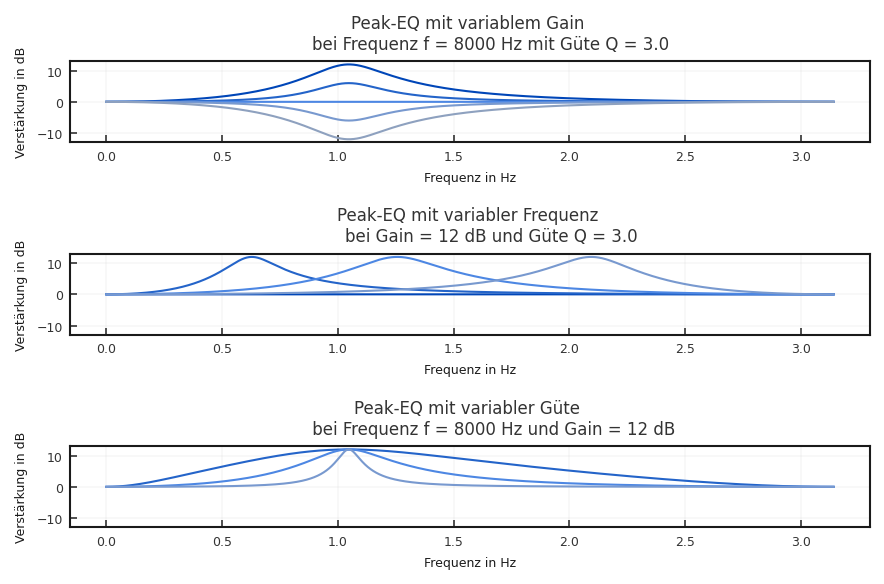
Fig. 6.5 Equalizerübertragungskurve bei Veränderung der Güte#
Starten des interaktiven Programms -
Filter_Peak_EQ.pyinjupyterbook/code/interactive_programs/Mit Slidern Parameter einstellen
Es gibt auch noch spezielle Filter für den Hoch- und Tiefpassbereich, die als Kuhschwanzfilter (Shelving-Filter) bezeichnet werden. Hierbei stehen nur die zwei Parameter Frequenz und Verstärkung bzw. Abschwächung zur Verfügung.
# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0 18.02.2022
#
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------
import matplotlib
import numpy
from scipy import signal
from matplotlib import pyplot
from matplotlib.widgets import RadioButtons
from matplotlib.widgets import Slider
# determine where we're running from and set paths accordingly
try:
if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
prefix = ''
except:
prefix = '../../'
matplotlib.style.use(f'{prefix}sv.mplstyle')
def getShelvingEQ(f_0, Gain_dB, shelf_type, fs):
'''
calculates filter coefficients of a shelving equalizer
with the given parameters
Parameters:
-----------
f_0 : int
peak frequency in Hz
gain_dB : int
dB gain at peak
shelf_type : str
"high" for high-shelf, anything else for low shelf
fs : int
sampling frequency
'''
K = numpy.tan(2*numpy.pi*f_0/(fs*2))
a = [0]*3
b = [0]*3
den = 1
if (shelf_type == "high"): # High-Shelf
if (Gain_dB > 0):
V0 = 10**(Gain_dB/20)
den = 1 + numpy.sqrt(2)*K + K*K
b[0] = V0 + numpy.sqrt(2*V0)*K+K*K
b[1] = 2 * (K*K - V0)
b[2] = V0 - numpy.sqrt(2*V0)*K + K*K
a[0] = 1
a[1] = 2 * (K*K - 1)
a[2] = 1 - numpy.sqrt(2)*K + K*K
b /= den
a[1:] /= den
else:
V0 = 10**(-Gain_dB/20)
den = V0 + numpy.sqrt(V0*2)*K + K*K
b[0] = 1 + numpy.sqrt(2)*K + K*K
b[1] = 2 * (K*K - 1)
b[2] = 1 - numpy.sqrt(2)*K + K*K
b /= den
den = 1 + numpy.sqrt(2/V0)*K + K*K/V0
a[0] = 1
a[1] = 2 * (K*K/V0 - 1)
a[2] = (1 - numpy.sqrt(2/V0)*K + K*K/V0)
a[1:] /= den
else: #Low-Shelf 0 or default for != 1
if (Gain_dB > 0):
V0 = 10**(Gain_dB/20)
den = 1 + numpy.sqrt(2)*K + K*K
b[0] = 1 + numpy.sqrt(2*V0)*K + V0*K*K
b[1] = 2 * (V0*K*K - 1)
b[2] = 1 - numpy.sqrt(2*V0)*K + V0*K*K
a[0] = 1
a[1] = 2 * (K*K - 1)
a[2] = 1 - numpy.sqrt(2)*K + K*K
else:
V0 = 10**(-Gain_dB/20)
den = 1 + numpy.sqrt(V0*2)*K + V0*K*K
b[0] = 1 + numpy.sqrt(2)*K + K*K
b[1] = 2 * (K*K - 1)
b[2] = 1 - numpy.sqrt(2)*K + K*K
a[0] = 1
a[1] = 2 * (V0*K*K - 1)
a[2] = 1 - numpy.sqrt(V0*2)*K + V0*K*K
b /= den
a[1:] /= den
return b, a
#parameters
gains = [12, 6, 0, -6, -12]
fs = 48000
f_c = 8000
shelf_types = ["low", "high"]
fig, (ax_gain, ax_freq) = pyplot.subplots(2, 1)
for gain in gains:
for ftype in shelf_types:
b, a = getShelvingEQ(f_c, gain, ftype, fs) # get filter coefficients
print(b, a)
w, h = signal.freqz(b, a, fs=fs) # calculate impulse response
#with numpy.errstate(divide='ignore'):
h_db = 20*numpy.log10(numpy.abs(h)) # dB
ax_gain.plot(w, h_db)
ax_gain.set(ylim=[-13, 13], xlabel='Frequenz in Hz',ylabel='Verstärkung in dB',
title=f'Shelf-EQs variablem Gain \n bei Grenzfrequenz f = {f_c} Hz')
freqs = [0, fs/10, fs/5, fs/3]
gain = 12
for f_c in freqs:
for ftype in shelf_types:
b, a = getShelvingEQ(f_c, gain, ftype, fs) # get filter coefficients
print(b, a)
w, h = signal.freqz(b, a, fs = fs) # calculate impulse response
with numpy.errstate(divide='ignore'):
h_db = 20*numpy.log10(numpy.abs(h)) # dB
ax_freq.plot(w, h_db)
ax_freq.set(ylim=[-13, 13], xlabel='Frequenz in Hz',ylabel='Verstärkung in dB',
title=f'Shelf-EQs mit variabler Grenzfrequenz \n bei Gain = {gain} dB')
pyplot.tight_layout()
pyplot.show()
# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("EQ_ShelvParam", fig, display=False)
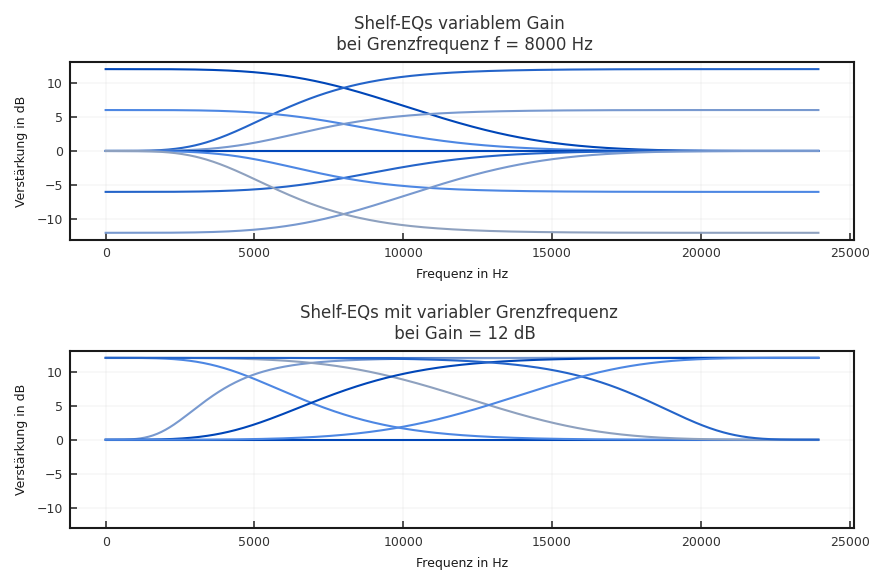
Fig. 6.6 Equalizerübertragungskurven eines Hoch bzw. Tiefpasskuhschwanzfilters bei Veränderung der Verstärkung und Frequenz#
Starten des interaktiven Programms -
Filter_Shelving_EQ.pyinjupyterbook/code/interactive_programs/Mit Slidern Parameter einstellen
Im Gegensatz zu den vollparametrischen EQs sind bei einem Terzband-Equalizer die Frequenzen und Güten festgelegt. Der Nutzer hat nur einen Einfluss auf die Verstärkung oder Absenkung. Der Vorteil dieser Equalizer ist ihre einfache Bedienung und die Möglichkeit sofort zu sehen, welche Frequenzveränderungen vorgenommen werden. Die Mittenfrequenzen der Filter sind standardisiert:
import pandas
df_oktav = pandas.DataFrame(data = {
'index':[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4],
'Frequenz (Hz)':[31.5, 63, 125, 250, 500, 1000, 2000, 4000, 8000, 16000]})
df_terz = pandas.DataFrame(data = {
'index': [-16, -15, -14, -13, -12, -11, -10, -9, -8, -7, -6,
-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13] ,
'Frequenz (Hz)': [25,31.5, 40, 50, 63, 80, 100, 125, 160, 200, 250,
315, 400, 500, 630, 800,1000,1250,1600,2000,2500,
3150,4000,5000,6300,8000,10000,12500,16000,20000]})
df_oktav = df_oktav.set_index('index')
df_terz = df_terz.set_index('index')
glue("df_oktav", df_oktav, display=False)
glue("df_terz", df_terz, display=False)
| Frequenz (Hz) | |
|---|---|
| index | |
| -5 | 31.5 |
| -4 | 63.0 |
| -3 | 125.0 |
| -2 | 250.0 |
| -1 | 500.0 |
| 0 | 1000.0 |
| 1 | 2000.0 |
| 2 | 4000.0 |
| 3 | 8000.0 |
| 4 | 16000.0 |
| Frequenz (Hz) | |
|---|---|
| index | |
| -16 | 25.0 |
| -15 | 31.5 |
| -14 | 40.0 |
| -13 | 50.0 |
| -12 | 63.0 |
| -11 | 80.0 |
| -10 | 100.0 |
| -9 | 125.0 |
| -8 | 160.0 |
| -7 | 200.0 |
| -6 | 250.0 |
| -5 | 315.0 |
| -4 | 400.0 |
| -3 | 500.0 |
| -2 | 630.0 |
| -1 | 800.0 |
| 0 | 1000.0 |
| 1 | 1250.0 |
| 2 | 1600.0 |
| 3 | 2000.0 |
| 4 | 2500.0 |
| 5 | 3150.0 |
| 6 | 4000.0 |
| 7 | 5000.0 |
| 8 | 6300.0 |
| 9 | 8000.0 |
| 10 | 10000.0 |
| 11 | 12500.0 |
| 12 | 16000.0 |
| 13 | 20000.0 |
Für bestimmte Anwendungen (z.B. Synthesizer) werden auch manchmal Filter verwendet, die in ihrer Grundcharakteristik den Sperrfiltern entsprechen, aber zusätzlich in der Nähe der Grenzfrequenz eine Verstärkung einbringen. Diese Verstärkungsfrequenzen kommen bei natürlichen Musikinstrumenten ebenfalls häufig vor. Man spricht in diesem Fall von Resonanzfrequenzen, da bestimmte Signalanteile im Filter eine starke Resonanz finden.
6.2. Realisierungsformen#
Wir haben gesehen, dass es eine Vielzahl von unterschiedlichen Filtereinsatzmöglichkeiten gibt. Bisher wurde aber keinerlei Hinweis auf die Realsierungsformen gegeben. Aus der Beschreibung von Systemen kennen wir zwei unterschiedliche Systemarten. Die Systeme mit Rückkopplung (rekursiv) und ohne Rückkopplung (transversal). Als Bezeichnung hatten wir Infinite Impulse Response (IIR) bzw. Finite Impulse Response (FIR) Systeme eingeführt. Und genau diese Bezeichnungen kennzeichnen auch die beiden grundsätzlichen Realisierungsformen von Filtern.
6.2.1. FIR-Filter#
Die Anwendung von FIR-Filtern ist ausschließlich durch digitale Signalverarbeitung möglich, da eine Realisierung in Analogtechnk mit elektrischen Bauelementen nicht möglich ist. FIR-Filter zeichnen sich durch einige positive Eigenschaften aus. In erster Linie kann die Stabilität immer garantiert werden. Alle FIR-Filter sind stabil. Weiterhin ist es möglich mit FIR-Systemem Filter zu realisieren, die nur den Betragsfrequenzgang verändern und sonst nur eine zeitliche Verzögerung des Signals bewirken. Die zeitliche Verzögerung macht sich in der Übertragungsfunktion durch eine lineare Phase deutlich. Diese Filter werden deshalb linearphasig genannt.
6.2.1.1. Beschreibung als Blockdiagramm#
Bisher haben wir FIR-Systeme nur als Differenzengleichung oder als z-Übertragungsfunktion kennen gelernt. Um die noch folgende Implementierung zu ermöglichen ist eine andere Darstellung aber hilfreicher. Schaut man sich die Differenzengleichung für ein FIR-Filter genauer an, so erkennt man, dass man 3 verschiedene Bauteile benötigt werden:
Addierer
Multiplizierer
Einen Verzögerungseinheit, die das Signal um genau ein Sample \(T\) verzögert. Dies kann durch ein einfaches Speicherelement geschehen.
Diese 3 Elemente werden im folgenden durch die in Abbildung 6.7 gezeigten Symbole beschrieben.
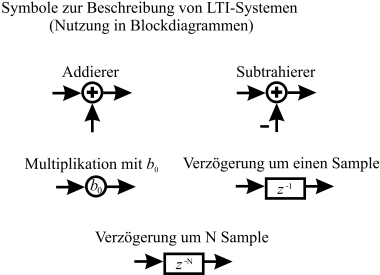
Fig. 6.7 Symbole zur Darstellung von Filterstrukturen als Blockdiagramm.#
Beispielsweise ergibt sich für ein FIR-System erster Ordnung, das durch \(y(k) = b_0 x(k) + b_1 x(k-1)\) beschrieben ist, das Blockschaltbild in Abbildung 6.8).
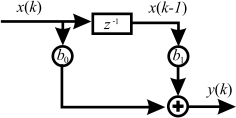
Fig. 6.8 Blockdiagramm eines FIR-Filters 1. Ordnung#
Zur Realisierung eines allgemeinen FIR-Filters muss das allgemeine Blockschaltbild genauer betrachtet werden (siehe Abbildung 6.9).
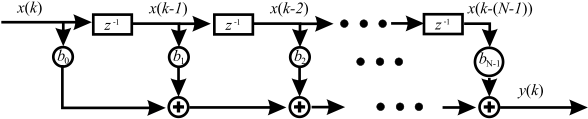
Fig. 6.9 Allgemeine FIR-Filter Struktur.#
Es wird deutlich, dass wir bei \(N\) Koeffizienten \(N-1\) Speicherelemente benötigen, die die jeweilige Vergangenheit von \(x(k)\) speichern.
Um einen Ausgangswert \(y(k)\) zu berechnen, muss die Summe
berechnet werden. Abschließend wird der Speicher um eine Stelle weiter geschoben. Gleichung (6.1) ist bereits von der Faltung bekannt. Somit ist ein FIR-Filter also eine andere Bezeichnung für ein System zur Faltung.
6.2.2. FIR-Filter Design#
Nachdem die Strukturen zur Realisierung von Filtern bekannt sind, fehlt noch die Bestimmung der einzelnen Filterkoeffizienten. Es muss also überlegt werden, wie aus einem bestimmten Entwurf des Filters im Frequenzbereich, geeignete Koeffizienten im Zeitbereich berechnet werden können. Dazu betrachten wir zunächst nur die FIR-Filter. Es sind verschiedene Verfahren bekannt. Die beiden am häufigsten Methoden sollen im weiteren genauer erläutert werden.
6.2.2.1. Fenster-Methode#
Aus dem Abschnitt über Spektren ist uns bekannt, dass wir zu einer Zeitfolge mit Hilfe der DTFT ein Spektrum berechnen können, dass in \(2\pi\) periodisch ist. Zu dieser Hintransformation gibt es auch die korrespondierende Rücktransformation die als
definiert ist. Somit ist es natürlich auch möglich zu einem bestimmten Frequenzentwurf eine zugehörige Zeitfolge zu berechnen. Nehmen wir beispielsweise an, wir suchen die Koeffizienten, um ein ideales Tiefpassfilter mit der Grenzfrequenz \(\Omega_\text{g}\) zu realisieren. Die Definition der Übertragungsfunktion ist somit
Für die gesuchten Filterkoeffizienten ergibt sich
Problematisch an diesem Ergebnis ist zum einen, dass sich die gefundene Koeffizienten unendlich ausdehnen und zum anderen, dass das Filter auch noch nicht-kausale Anteile enthält. Aus dem ersten Grund muss immer eine Begrenzung vorgenommen werden. Das heißt die gefundenen Koeffizienten werden nach einer bestimmten Länge zu beiden Seiten der Zeitachse gleichmäßig abgeschnitten. Dies führt nicht mehr zum idealen Tiefpass, sondern zu einer Approximation. Der sich ergebende Fehler kann aus der Überlegung zur Spektrumsanalyse ersehen werden. Die Begrenzung entspricht einer Gewichtung der Filterkoeffizienten mit einem Rechteck-Fenster. Diese Multiplikation führt im Frequenzbereich zu einer Faltung mit der Übertragungsfunktion des Rechtecks. Für den idealen Tiefpass hat das zwei Konsequenzen. Erstens ist der Übergang vom Durchlass- zum Sperrbereich nicht mehr unendlich steil und zweitens enstehen an der Übergangsstelle Überschwinger. Vergrößert man nun die Länge des Ausschnitts, so wird der Übergangsbereich schmaller, und die Überschwinger konzentrieren sich an der Übergangsstelle, aber die Höhe der Überschwinger bleiben gleich (siehe Abbildung 6.10 ). Dies wird als Gibbs’sches Phänomen bezeichnet.
# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0 18.02.2022
#
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------
import matplotlib
import numpy
from matplotlib import pyplot
# determine where we're running from and set paths accordingly
try:
if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
prefix = ''
except:
prefix = '../../'
matplotlib.style.use(f'{prefix}sv.mplstyle')
fig, (ax_si, ax_spec) = pyplot.subplots(1,2)
samples = numpy.linspace(-100, 100, 201)
si = [0]*len(samples)
mid = int(numpy.floor(len(samples)/2))
fs = 1000
f0 = 100
for idx in range(len(samples)):
if (samples[idx]!=0):
si[idx] = numpy.sin(2*numpy.pi * f0 * samples[idx]/fs)/(2*numpy.pi*samples[idx]*f0/fs)
else:
# si(0) = 1 to avoid division by zero
si[idx] = 1
# cut si-function
si_short = si[(mid-25):(mid+25)]
samples_short = samples[(mid-25):(mid+25)]
#ax_si = pyplot.subplot(1, 2, 1)
ax_si.plot(samples, si, linestyle='dotted')
ax_si.plot(samples_short, si_short)
ax_si.set(xlabel='Folgenkindex k ->', ylabel='Amplitude x(k)',
title='SI-Funktion')
ax_si.set_xlim([-100, 100])
# zero padding, for display resolution
si_short = [0]*100 + si_short + [0]*100
si = [0]*100 + si + [0]*100
spectrum_short = numpy.fft.fft(si_short)
spectrum = numpy.fft.fft(si)
w = numpy.linspace(0, 2, len(si))
w_short = numpy.linspace(0, 2, len(si_short))
#ax_spec = pyplot.subplot(1, 2, 2)
ax_spec.plot(w_short, 20 * numpy.log10(abs(spectrum_short)),
linestyle='dotted')
ax_spec.plot(w, 20 * numpy.log10(abs(spectrum))) # dB spectrum
ax_spec.set(xlabel='Frequenz normalisiert mit w/pi', ylabel='Amplitude in dB',
title='Spektrum', xlim=([0, 0.4]))
pyplot.show()
# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("GippsPheanomen", fig, display=False)
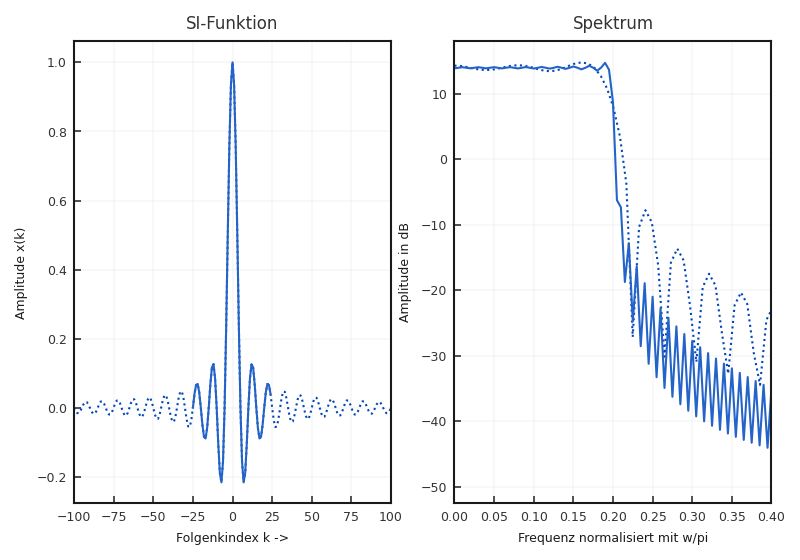
Fig. 6.10 Veranschaulichung des Gibbs’schen Phänomens am Beispiel eines Tiefpassfilters.#
Die Ursache hierfür ist in der Übertragungsfunktion des Rechteckfensters zu suchen. Betrachtet man diese Funktion für die beiden betrachteten Längen, so erkennt man die Konzenzentration der Überschwinger bei der Frequenz Null. Die Höhe der Überschwinger bleibt aber identisch. Genau dieses Verhalten wird durch die Faltung im Frequenzbereich auf die Übertragungsfunktion des idealen Tiefpasses aufgeprägt. Man kann aber zeigen, dass die Approximation im Sinne des kleinsten Fehlerquadrates Minimum Mean Square Error (MMSE) über alle Frequenzen optimal ist [KK98].
Um die nicht-kausalen Anteile zu beseitigen ist zusätzlich noch eine zeitliche Verschiebung der gefundenen Filterkoeffizienten notwendig. Diese Verschiebung führt dann, wie man durch den Verschiebungssatz der Fourier-Transformation sieht, zu einer linearen Phase des entworfenen Tiefpasses.
Zur Vermeidung der Überschwinger (Ripple) können nun dieselben Techniken verwendet werden, die auch die Spektralanalyse verbessert haben. Eine Nutzung der dort vorgestellten Fensterfunktionen führt auf eine geringere Ausprägung der Ripple, wobei gleichzeitig der Übergangsbereich zwischen Durchgangs- und Sperrbereich zunimmt. Um das zu veranschaulichen, ist in Abbildung 6.11 der Entwurf eines Filters mit unterschiedlichen Fensterfunktionen gezeigt. Man erkennt deutlich, dass mit zunehmendem Übergangsbereich die Überschwinger abnehmen, wobei diese bei Nutzung der Fensterfunktionen nur noch im Sperrbereich deutlich zu erkennen sind.
# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0 18.02.2022
#
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------
import matplotlib
import numpy
from scipy import signal
from matplotlib import pyplot
# determine where we're running from and set paths accordingly
try:
if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
prefix = ''
except:
prefix = '../../'
matplotlib.style.use(f'{prefix}sv.mplstyle')
fig, (ax_51, ax_201) = pyplot.subplots(1, 2)
eps = numpy.finfo(float).eps # for slight offset to avoid division by 0
f_s = 48000
f_g = 4800 # Hz, cuttoff frequency
trans_width = 1200 # Hz, Width of transition from pass band to stop band
# filter length 51
N = 51 # Size of the FIR filter.
idxs = numpy.linspace(numpy.ceil(-N/2), numpy.floor(N/2), N)
# Remez filter design
taps = signal.remez(N, [0, f_g, f_g + trans_width, 0.5*f_s], [1, 0], Hz=f_s)
w, h = signal.freqz(taps, [1], worN=2000)
w = w/numpy.pi
# Von Hann filter design
w_rad = 2*numpy.pi*f_g/f_s # cutoff freq in rang od 0 -> 2*pi
# designing the filter
rect_window_51 = w_rad/numpy.pi * numpy.sin(w_rad*idxs+eps)/(w_rad*idxs+eps)
von_hann_window = [0]*N
for idx in range(N):
von_hann_window[idx] = 0.5 - 0.5*numpy.cos(2*numpy.pi*idx/N)
window_51 = numpy.array(rect_window_51) * numpy.array(von_hann_window)
spectrum = numpy.fft.fft(numpy.concatenate((window_51, [0]*1000)))
mid = numpy.floor(len(spectrum)/2)
# shift area from pi -> 2pi to -pi -> 0
spectrum = numpy.concatenate([spectrum[int(mid):], spectrum[:int(mid)]])
# dB maximum = 0dB
spectrum_abs = 20*numpy.log10(numpy.abs(spectrum)/numpy.abs(spectrum).max())
freqs_fft = numpy.linspace(-1, 1, len(spectrum_abs)) # freq bins, for plotting
ax_51.plot(w, 20*numpy.log10(numpy.abs(h)))
ax_51.plot(freqs_fft, spectrum_abs, linestyle='--')
ax_51.set(xlabel='Frequenz in rad/s', ylabel='Pegel in dB', xlim=[0, 0.4],
ylim=[-100, 5], title='Filterlänge 51')
# filter length 201
# -----------------
N = 201 # Size of the FIR filter.
idxs = numpy.linspace(numpy.ceil(-N/2), numpy.floor(N/2), N)
taps = signal.remez(N, [0, f_g, f_g + trans_width, 0.5*f_s], [1, 0], Hz=f_s)
w, h = signal.freqz(taps, [1], worN=2000)
w = w/numpy.pi
# Von Hann
w_rad = 2*numpy.pi*f_g/f_s # cutoff freq in rang od 0 -> 2*p
# designing the filter
rect_window_51 = w_rad/numpy.pi * numpy.sin(w_rad*idxs+eps)/(w_rad*idxs+eps)
von_hann_window = [0]*N
for idx in range(N):
von_hann_window[idx] = 0.5 - 0.5*numpy.cos(2*numpy.pi*idx/N)
window_201 = numpy.array(rect_window_51) * numpy.array(von_hann_window)
spectrum = numpy.fft.fft(numpy.concatenate((window_201, [0]*1000)))
mid = numpy.floor(len(spectrum)/2)
# shift area from pi -> 2pi to -pi -> 0
spectrum = numpy.concatenate([spectrum[int(mid):], spectrum[:int(mid)]])
# dB maximum = 0dB
spectrum_abs = 20*numpy.log10(numpy.abs(spectrum)/numpy.abs(spectrum).max())
freqs_fft = numpy.linspace(-1, 1, len(spectrum_abs)) # freq bins, for plotting
ax_201.plot(w, 20*numpy.log10(numpy.abs(h)))
ax_201.plot(freqs_fft, spectrum_abs, linestyle='--')
ax_201.set(xlabel='Frequenz in rad/s', ylabel='Pegel in dB', xlim=[0, 0.4],
ylim=[-100, 5], title='Filterlänge 201')
pyplot.show()
# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("BspFensterEntwurf", fig, display=False)
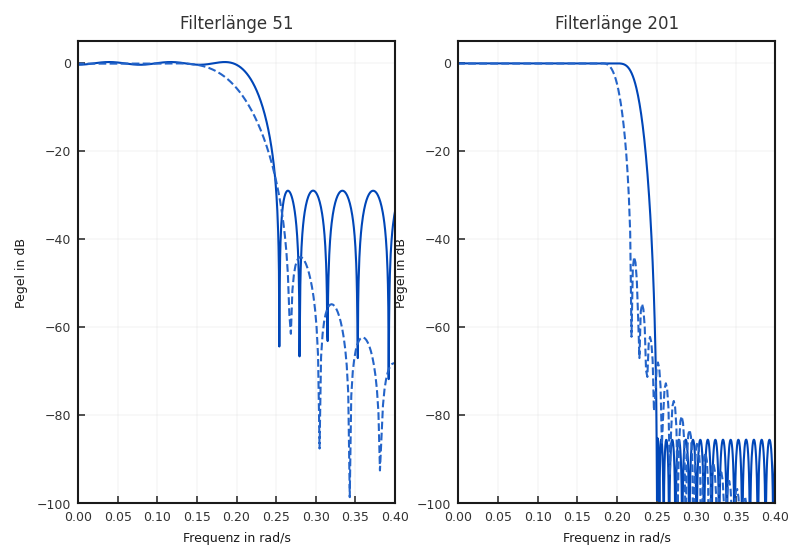
Fig. 6.11 Beispiel eines Tiefpass-Entwurfes mit Rechteck und Hann-Fenster unterschiedlicher Länge. \(f_\text{g} = \Omega_\text{g} = 0{,}2\pi\).#
6.2.2.2. Parks-McClellan#
Im letzten Abschnitt wurde eine optimale Lösung vorgestellt, die den mittleren Fehler über das Gesamtspektrum minimiert. Dabei hat sich aber der Fehler an der Übergangsstelle konzentriert. Eine weitere optimale Lösung ist, den Fehler über alle Frequenzen gleich zu verteilen. Die verbleibende Fehlergröße ist dabei nur von der gewählten Ordnung des Filters abhängig. Zur Lösung dieses Problems wurde von Parks und McClellan der sog. Remez-Algorithmus entwickelt, der zur optimalen Lösung konvergiert. Der Restfehler ist dabei minimal für alle Frequenzen. Diese Minimierung des maximalen Fehlers wird auch als Tschebyscheff-Lösung bezeichnet.
Um die Lösung zu verdeutlichen und die Unterschiede zur Fenster-Methode
heraus zu arbeiten, ist in Abbildung 6.13
ein Entwurf eines Tiefpass-Filters
mittels Remez-Entwurfsverfahren und mittels Fenster-Entwurfs mit
Hann-Fenster gegenüber gestellt. Wir erkennen, dass bei gleicher Ordnung
das Remez-Verfahren eine insgesamt bessere Sperrdämpfung aufweist.
Dies bedeutet im Umkehrschluss, dass bei einer im Entwurf
spezifizierten Sperrdämpfung die Ordnung des resultierenden Filters beim
Remez-Verfahren deutlich kleiner ist. Für die konkrete Realisierung
bedeutet dies eine deutliche Aufwandsreduktion.
# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0 18.02.2022
#
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------
import matplotlib
import numpy
from scipy import signal
from matplotlib import pyplot
# determine where we're running from and set paths accordingly
try:
if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
prefix = ''
except:
prefix = '../../'
matplotlib.style.use(f'{prefix}sv.mplstyle')
fig, (ax_51, ax_201) = pyplot.subplots(1, 2)
eps = numpy.finfo(float).eps # for slight offset to avoid division by 0
f_s = 48000
f_g = 4800 # cutoff frequency
trans_width = 1200 # Hz, Width of transition from pass band to stop band
# filter length 51
# ----------------
N = 51 # Size of the FIR filter.
idxs = numpy.linspace(numpy.ceil(-N/2), numpy.floor(N/2), N)
# Remez filter design
taps = signal.remez(N, [0, f_g, f_g + trans_width, 0.5*f_s], [1, 0], Hz=f_s)
w, h = signal.freqz(taps, [1], worN=2000)
w = w/numpy.pi
# boxcar window filter design
w_rad = 2*numpy.pi*f_g/f_s # cutoff freq in rang od 0 -> 2*pi
# designing the filter
rect_window_51 = w_rad/numpy.pi * numpy.sin(w_rad*idxs+eps)/(w_rad*idxs+eps)
spectrum = numpy.fft.fft(rect_window_51, n=2000)
mid = numpy.floor(len(spectrum)/2)
# shift area from pi -> 2pi to -pi -> 0
spectrum = numpy.concatenate([spectrum[int(mid):], spectrum[:int(mid)]])
# dB maximum = 0dB
spectrum_abs = 20*numpy.log10(numpy.abs(spectrum)/numpy.abs(spectrum).max())
freqs_fft = numpy.linspace(-1, 1, len(spectrum_abs)) # freq bins, for plotting
ax_51.plot(w, 20*numpy.log10(numpy.abs(h)))
ax_51.plot(freqs_fft, spectrum_abs, linestyle='--')
ax_51.set(xlabel='Frequenz in rad/s', ylabel='Pegel in dB', xlim=[0, 0.4],
ylim=[-100, 5], title='Filterlänge 51')
# filter length 201
# -----------------
N = 201 # Size of the FIR filter
idxs = numpy.linspace(numpy.ceil(-N/2), numpy.floor(N/2), N)
# Remez filter design
taps = signal.remez(N, [0, f_g, f_g + trans_width, 0.5*f_s], [1, 0], Hz=f_s)
w, h = signal.freqz(taps, [1], worN=2000)
w = w/numpy.pi
# boxcar window filter design
w_rad = 2*numpy.pi*f_g/f_s # cutoff freq in rang od 0 -> 2*pi
# designing the filter
rect_window_201 = w_rad/numpy.pi * numpy.sin(w_rad*idxs+eps)/(w_rad*idxs+eps)
spectrum = numpy.fft.fft(numpy.concatenate((rect_window_201, [0]*1000)))
mid = numpy.floor(len(spectrum)/2)
# shift area from pi -> 2pi to -pi -> 0
spectrum = numpy.concatenate([spectrum[int(mid):], spectrum[:int(mid)]])
# dB maximum = 0dB
spectrum_abs = 20*numpy.log10(numpy.abs(spectrum)/numpy.abs(spectrum).max())
freqs_fft = numpy.linspace(-1, 1, len(spectrum_abs)) # freq bins, for plotting
ax_201.plot(w, 20*numpy.log10(numpy.abs(h)))
ax_201.plot(freqs_fft, spectrum_abs, linestyle='--')
ax_201.set(xlabel='Frequenz in rad/s', ylabel='Pegel in dB', xlim=[0, 0.4],
ylim=[-100, 5], title='Filterlänge 201')
pyplot.show()
# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("BspFensterRemez", fig, display=False)
Fenster Entwurf

Fig. 6.12 Beispiel eines Tiefpass-Entwurfes mit Rechteck und Hann-Fenster unterschiedlicher Länge. \(f_\text{g} = \Omega_\text{g} = 0{,}2\pi\).#
Remez Fenster
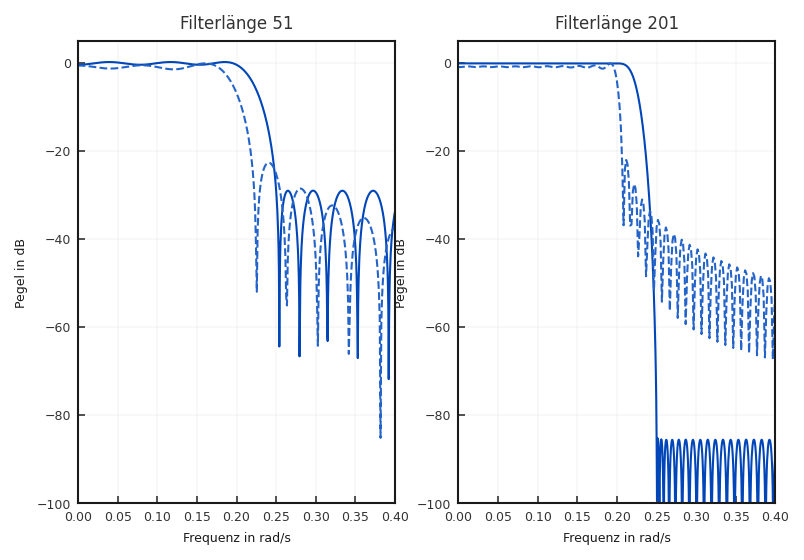
Fig. 6.13 Beispiel eines Tiefpass-Entwurfes mit dem Remez-Algorithmus und der Fenster-Methode unterschiedlicher Länge. \(f_\text{g} = \Omega_\text{g} = 0{,}2\pi\).#
To Do
Aufzeigen der Fenstermethode für allgemeine Übertragungsfunktionen, Design im Frequenzbereich, IFFT und dann Ausschneiden, je nach Ordnung
6.2.2.3. Linearphasige Filter#
Linearphasigkeit ist eine interessante Eigenschaft in der Nachrichtentechnik, da mit Ihrer Hilfe ein Signal gefiltert werden kann, ohne weitere Phasenverzerrungen einzuführen. Weiterhin führt die Linearphasigkeit dazu, dass alle Frequenzanteile des Signals um einen konstanten Betrag verzögert werden. Diese Verzögerung wird als Gruppenlaufzeit bezeichnet und ist über
als Ableitung der Phase zur Frequenz definiert.
Wir haben bereits für das einfache Filter mit der Impulsantwort \(h(k) = [1\:\: 1]\) festgestellt, dass es sich um einen Tiefpass mit linearer Phase handelt. Diese Eigenschaft beruht drauf, dass die Nullstellen dieses FIR-Systems nur auf dem Einheitskreis liegen. Zusätzlich sind aber auch alle Systeme linearphasig die am Einheitskreis gespiegelte Nullstellen aufweisen. Es muss also gelten, dass zu jeder Nullstelle \(z_i\) die nicht auf dem Einheitskreis liegt eine weitere Nullstelle mit \(z_{\ell} = 1/z_i\) existiert.
Diese Symmetrie in der Pol-Nullstellenebene führt zu bestimmten Eigenschaften bei den Koeffizienten. Man kann zeigen, dass 4 verschiedene Möglichkeiten existieren, linearphasige FIR-Filter zu realisieren [KK98]. Diese unterscheiden sich darin, ob die Ordnung gerade oder ungerade ist und ob die Koeffizienten zur Mitte des Filters achsen- oder punktsymmetrisch sind. Daraus ergeben sich folgende Abhängigkeiten:
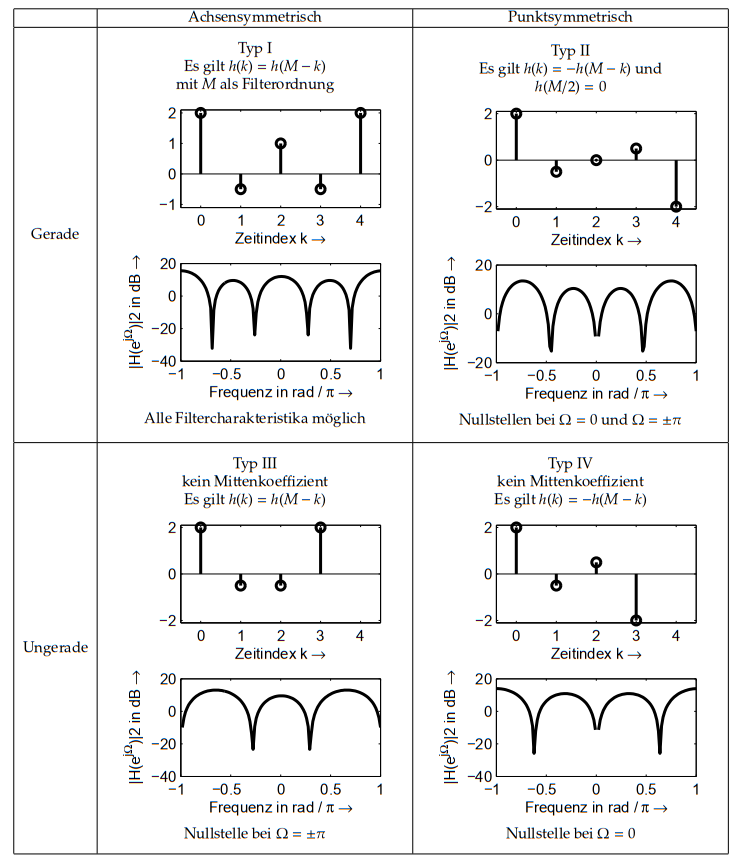
Aus diesen vier Symmetrieanordnungen resultieren einige Eigenschaften für die Übertragungsfunktion. Nur mit einem Filter Typ I lassen sich alle Grundfiltercharakteristika erzeugen. Bei den anderen Typen ergeben sich feste Werte für bestimmte Punkte der Übertragungsfunktion. So ist für den Typ II immer eine Nullstelle bei \(\Omega = 0\) und \(\Omega = \pi\), während der Typ III immer eine Nullstelle bei \(\Omega = \pm \pi\) besitzt. Typ IV dagegen hat immer eine Nullstelle bei \(\Omega = 0\)
Dies hat natürlich Konsequenzen für den Entwurf von linearphasigen FIR-Filtern. So sollte man nie versuchen einen Hochpass zu entwerfen und gleichzeitig Typ II oder Typ III verwenden wollen. Das heißt, man sollte darauf achten, ob das gewünschte Filterverhalten, auch mit dem Entwurfsvorgaben zusammen passen.
6.2.2.4. Minimalphasige FIR-Filter#
Eine weitere besondere Klasse an FIR-Filtern sind sogenannte
minimalphasige Filter. Das heisst, dieses Filter realisiert eine
bestimmte Betragsübertragungsfunktion mit der minimalen Phase.
Es zeigt sich dass sich dieser Filtertyp genau dann ergibt, wenn alle Nullstellen
innerhalb des Einheitskreises liegen. Eine Realisierung ist also
über ein Berechnen aller Nullstellen und deren Spiegelung am
Einheitskreis möglich, da sich so nur die Phase aber nicht das
Betragsverhalten ändert. Die Zerlegung von Filtern sehr hoher
Ordnung ist numerisch aufwändig und durch mögliche
Rundungsfehler nicht immer stabil.
Eine andere Methode nutzt die besondere Eigenschaft minimalphasiger Filter, dass es eine direkte Verknüpfung zwischen dem Betrag und der Phase gibt. Hierzu wird die sog. Hilbert-Transformation verwendet, die aber erst in einem späteren Abschnitt intensiver eingeführt wird. An dieser Stelle soll ein Vorstellen des Designalgorithmus genügen, um eine beliebige Betragsübertragungsfunktion (meist linearphasig, siehe Entwurfsmethoden) in einen minimalphasigen Entwurf zu überführen.
Gehen wir davon aus, dass die Betragsübertragungsfunktion \(|H(e^{(j \Omega)})|\) bekannt ist. Eine Logarithmierung dieses Spektrums ist möglich, so lange keine echte Nullstelle vorhanden ist, dies kann durch eine untere Schwelle gewährleistet werden. Dieses neue logarithmierte Spektrum wird mit Hilfe einer IDFT in den Zeitbereich transformiert. Da es sich um eine reelle gerade Funktion handelt, ergibt sich auch wieder eine reelle gerade Funktion. Diese Zeitbereichslösung wird nun so verändert, dass alle negativen Zeiten (oder positive Zeiten oberhalb von N/2, durch die Zirkulareigenschaft der DFT ist das gleichwertig) zu Null gesetzt und alle anderen Werte mit zwei multipliziert werden. Diese neue Funktion wird nun mit der FFT erneut in den Frequenzbereich transformiert. Um die Logarithmierung rückgängig zu machen wird für jeden Frequenzpunkt die Exponenten-Funktion angewendet. Eine erneute IFFT der resultierenden Funktion führt auf die Filterkoeffizienten, die das minimalphasige Filter repräsentieren. Abbildung 6.14 zeigt die Ergebnisse für einen einfaches Filter achter Ordnung bei vorgegebenem Betragsübertragungsverhalten.
# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0 18.02.2022
#
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------
import matplotlib
import numpy
from scipy import signal
from matplotlib import pyplot
# determine where we're running from and set paths accordingly
try:
if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
prefix = ''
except:
prefix = '../../'
matplotlib.style.use(f'{prefix}sv.mplstyle')
eps = numpy.finfo(float).eps # for slight offset to avoid division by 0
# create exemplary non-recursive filter coefficients (mirrored at unit circle)
b1 = [0.98]*4
b2 = [1.0/0.98]*4
h = numpy.poly(numpy.concatenate((b1, b2)))
h = [0.5, 0.7, 0.9, 1.1, 2, 1.1, 0.9, 0.7, 0.5]
h = numpy.array(h)/numpy.sum(h)
W, H = signal.freqz(b=h, a=1, worN=4*1024, whole=True)
fig, ((ax_H, ax_void), (ax_lin_zeit, ax_min_zeit),
(ax_lin_phase, ax_min_phase)) = pyplot.subplots(3, 2)
# create a linear phase filter from the exististing impulse response
log_H = numpy.log(numpy.abs(H)+eps)
h_c = numpy.fft.ifft(log_H).real
h_c[1 : int(len(h_c)/2)] *= 2
h_c[int(len(h_c)/2)+1 : ] = 0
H_min_log = numpy.fft.fft(h_c)
H_min = numpy.exp(H_min_log)
h_min = numpy.fft.ifft(H_min)
h_min = h_min[0:8]
ax_H.plot(W, 20*numpy.log10(numpy.abs(H)+eps))
ax_lin_zeit.stem(h, use_line_collection=True)
ax_min_zeit.stem(h_min, use_line_collection=True)
ax_lin_phase.plot(numpy.unwrap(p=numpy.angle(H)))
ax_min_phase.plot(numpy.unwrap(p=numpy.angle(H_min)))
pyplot.show()
# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("MinPhasenBsp", fig, display=False)
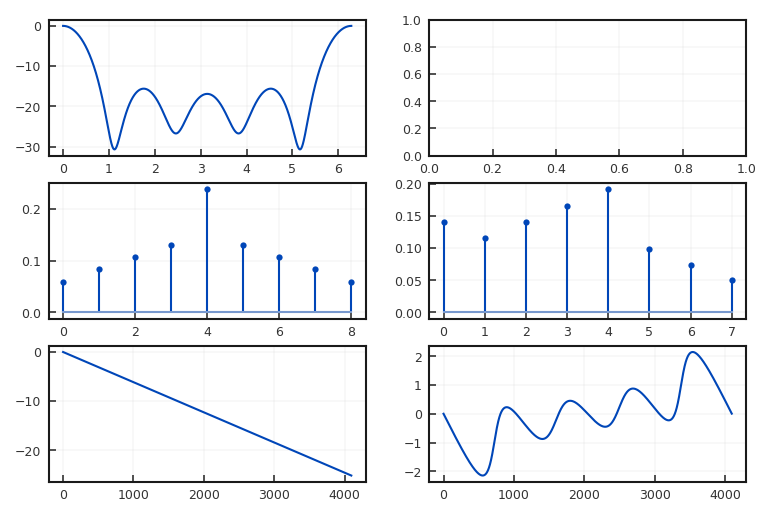
Fig. 6.14 Entwurf eines Filters mit gegebener Betragsübertragungsfunktion. a) als linearphasiges Filter und b) als minimalphasiges Filter.#
Eine mögliche Matlab- bzw. Python-Implementierung sieht folgendermaßen aus:
%v_H contains the magnitude vector of the desired filter
log_H = log(v_H+eps); % eps is the smallest positive number in matlab
% prevents log of zero
h_ceps = real(ifft(log_H)); % real for removing quantization error
h_ceps(2:length(h_ceps)/2) = 2*h_ceps(2:length(h_ceps)/2);
h_ceps(length(h_ceps)/2+1:end) = 0; % Setting to zero
H_min_log = fft(h_ceps);
H_min = exp(H_min_log);
v_h = real(ifft(H_min));
import numpy
#v_H contains the magnitude vector of the desired filter
eps = numpy.finfo(float).eps # eps is the smallest positive in python
log_H = numpy.log(numpy.abs(H)+eps) # eps prevents log of zero
h_c = numpy.fft.ifft(log_H).real # real for removing quantization error
h_c[1 : int(len(h_c)/2)] *= 2
h_c[int(len(h_c)/2)+1 : ] = 0 # Setting to zero
H_min_log = numpy.fft.fft(h_c)
H_min = numpy.exp(H_min_log)
h_min = numpy.fft.ifft(H_min)
6.2.3. IIR-Filter#
Im Gegensatz zu den FIR-Filtern haben IIR-Filter auch rekursive Anteile. Die Implementierung ist durch das Stabilitätsproblem sehr viel schwieriger. Gleichzeitig können sehr unterschiedliche Strukturen verwendet werden, die alle unterschiedliche Eigenschaften haben.
6.2.3.1. Beschreibung als Blockdiagramm#
Die Grundform des Blockdiagramms eines IIR-Filters ist in Abbildung 6.15 gezeigt.
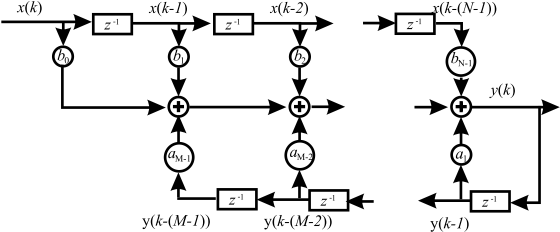
Fig. 6.15 IIR-Filter Struktur in Direkt Form I.#
Diese sehr grundlegende Struktur, die die Differenzengleichung geradlinig umsetzt wird als Direkt Form I bezeichnet. Sie ist einfach gängigen Programmiersprachen umzusetzen. Problematisch ist aber, dass bei einer höheren Ordnung \(N>8\) numerische Probleme auftreten, da bei vielen Filterentwürfen Filterkoeffizienten herauskommen, die im Zahlenbereich weit auseinander liegen und schlecht gleichzeitig in einem quantisierten Datenformat repräsentiert werden können.
Um dies zu vermeiden, wird im allgemeinen eine Zerlegung von Filtern höherer Ordnung in Filter 2. Ordnung vorgenommen. Diese werden dann Second Order Sections oder Biquads genannt. Eine kaskadierte Schaltung führt dann abschließend wieder zum Originaldesign, ohne die numerischen Schwierigkeiten zu beinhalten (siehe Abbildung 6.16).
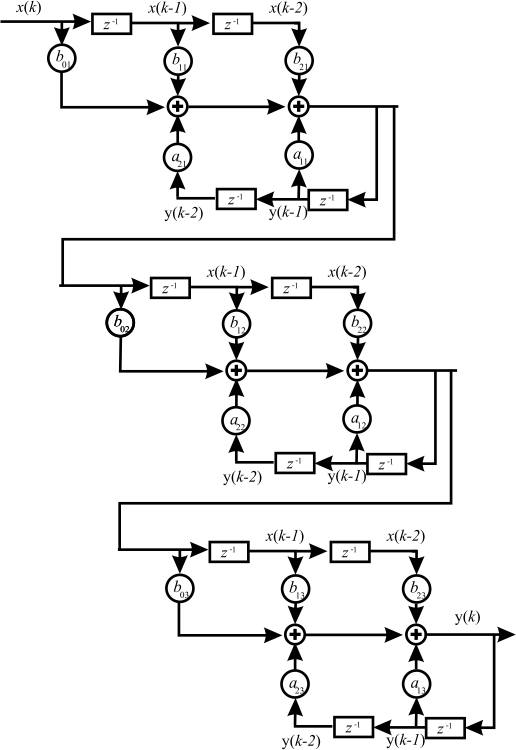
Fig. 6.16 Beispiel einer SOS-Zerlegung eines IIR-Filters 6.Ordnung.#
Mathematisch lässt sich die Zerlegung folgendermaßen darstellen:
Die Zusammenführung zweier Pole und Nullstellen sollte dabei immer so erfolgen, dass die Pole und Nullstellen möglichst dicht beieinander liegen (siehe Abbildung 6.17 ).
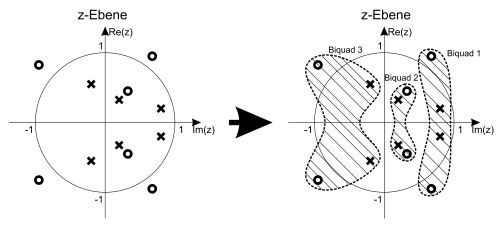
Fig. 6.17 Pol-Nullstellenzuordnung eines Filters 6.Ordnung zu drei Second Order Sections.#
6.2.3.2. Filterstrukturen für SOS#
Die Direkt Form I ist nicht die einzige Möglichkeit ein IIR-Filter zu realisieren. Um die anderen Strukturen zu verdeutlichen, konzentrieren wir uns auf die wichtigen SOS-Filter. Eine wichtige Anforderung an Realisierungen spielen die Anzahl der Multiplikationen und die Anzahl der benötigten Speicherplätze. Zusätzlich muss noch auf das numerische Verhalten bei einer quantisierten Datendarstellung geachtet werden. Den letzten Punkt werden wir zunächst nicht behandeln.
Eine Analyse der DF1 zeigt, dass wir fünf Multiplikationen und vier Speicherplätze benötigen. Durch Umstellen des Blockdiagramms lässt sich erkennen, dass es möglich ist die Speicher für den Transversal- und für den Rückführungszweig zusammen zu legen (siehe Abbildung 6.18 ). Diese Umstellung ist erlaubt, da wir zum einen den Transversal- und den Rückführungszweig als zwei getrennte Systeme auffassen können, zum anderen da beide Einzelsysteme LTI-Systeme sind und somit das Vertauschen keinen Einfluss auf das Übertragungsverhalten hat. Die jetzt parallel liegenden Speicherelemente können in einem abschließenden Schritt zusammen gefasst werden. Es ergibt sich die sogenannte Direkt-Form II mit einer minimalen Anzahl von zwei Speicherelementen. Strukturen mit minimaler Anzahl an Speicherelementen werden kanonisch genannt.
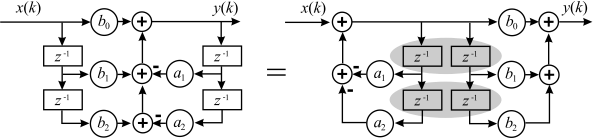
Fig. 6.18 Umwandlung einer DF1 Struktur in die kanonische DF2 Struktur. Die grau hinterlegten Verzögerungselemente können zu einem Element zusammen gefasst werden, da sie jeweils dasselbe Signal als Eingang haben.#
6.2.3.3. Vom Blockdiagramm zur Übertragungsfunktion#
To Do
Analyse des Block-Diagramms mit z-Trafo daraus folgend die Übertragungsfunktion , ??Wie geht es anders herum??
6.2.4. IIR-Filterdesign#
Um die Theorie des Entwurfs traditioneller IIR-Filter genauer zu
erläutern fehlen an dieser Stelle noch einige theoretische Konzepte. Abschnitt %s gibt alleridngs einen ersten Einblick in Entwurfsverfahren von IIR-Filtern auf Basis von Matlab.
Mit den bisherigen Erkenntnissen sind aber schon Lösungen für einige spezielle Filter möglich.
6.2.4.1. Notch-Filter#
To Do
Entwurf in z-Ebene durch Nullstellen auf dem Einheitskreis und Polstellen mit verringertem Radius und gleichem Winkel, Anwendungen bzw. Design Bsp.: DC Filter, Netzbrummfilter
6.2.4.2. Allpässe#
To Do
Wiederholung spezielles Pol-Nullstellendiagramm, Überlegungen zum Entwurf im z-Bereich, Anwendungen: Spezielle Filter
6.2.5. klassische IIR-Filterdesignmethoden#
Der Entwurf von IIR-Filtern erfolgt historisch bedingt etwas anders. Rekursive Filter sind sehr viel enger mit analogen Filtern verwandt. Eine Möglichkeit des IIR-Filterentwurfs besteht deshalb darin, einen analogen Entwurf durchzuführen und das Resultat in den Digitalbereich zu transformieren. Da bisher noch keine analogen Filter genauer besprochen wurden, soll an dieser Stelle nur Beispielhaft typische Lösungen und ihre Stärken und Schwächen gezeigt werden.
6.2.5.1. Butterworth-Filter#
Ziel des Butterworth-Entwurfs ist einen möglichst flachen
Durchlassbereich zu erhalten. Dies wird im analogen Entwurf durch
Nutzung einer Potenzfunktion gewährleistet (siehe Abschnitt
Analogentwurf) Aus diesem Grund wird dieser Entwurf auch als Maximum
Flat Design bezeichnet. In Matlab stehen die Befehle butter und
buttord für das Design zu Verfügung, wobei mit buttord zu einem
definierten Design die benötigten Entwurfsparameter bestimmt werden und
butter der eigentliche Entwurf ist. Angegeben werden meist zwei
Arbeitspunkte des Filters, zum einen bis zu welcher Frequenz der
Durchlassbereich definiert ist und welche Abstand von der 0dB Linie noch
als Durchlass gilt. Zum anderen ab welcher Frequenz eine bestimmte
Dämpfung erreicht werden muss (Sperrbereich). Da die Grenzfrequenz des
Butterworth-Filter durch die \(-3\)dB Grenze definiert, wird in Butterord
eine Anpassung an diese Frequenz vorgenommen.
Beispiel einer Filterspezifikation für normierte Frequenzen:
Durchlassbereich bis \(0.1\pi\) und maximale Dämpfung von \(0.2\)dB.
Sperrbereich ab \(02\pi\) und minimale Dämpfung von \(30dB\).
Der dazugehörige Code sieht dann wie folgt aus:
Pass_freq = 0.1; % Matlab uses normalized frequencies from 0..2
Pass_dB = 0.2;
Stop_freq = 0.2;
Stop_dB = 30;
[N,f_g] = buttord(Pass_freq,Stop_freq,Pass_dB,Stop_dB);
% Result is 7th Order and f_g = 0.1247
[b,a] = butter(N,f_g);
from scipy import signal
Pass_freq = 0.1
Pass_dB = 0.2
Stop_freq = 0.2
Stop_dB = 30
order, wn = signal.buttord(wp=Pass_freq, ws=Stop_freq, gpass=Pass_dB, gstop=Stop_dB, fs=f_s)
[b, a] = signal.butter(N=order, Wn=Pass_freq, output='ba')
6.2.5.2. Tschebyscheff-I-Filter#
Im Gegensatz zum Butterworth-Filter ist das Ziel des Tschebyscheff-I
Filters im Durchlassbereich die maximal zulässige Durchlassdämpfung
nicht zu überschreiten. Gleichzeitig wird aber erlaubt, diesen Bereich
bis zur Grenzfrequenz auszunutzen. Die Tschebyscheff-Optimierung hat
also immer zum Ziel den Maximalen Fehler zu minimieren. Der Entwurf wird
auch als Equiripple-Design bezeichnet. Dies führt zu einem Entwurf mit
geringerer Ordnung. Die zugehörigen Matlab-Befehle lauten cheb1ord und
cheby1. Für das Design-Beispiel ergibt sich der folgende Code.
Pass_freq = 0.1; % Matlab uses normalized frequencies from 0..2
Pass_dB = 0.2;
Stop_freq = 0.2;
Stop_dB = 30;
[N,f_g] = cheb1ord(Pass_freq,Stop_freq,Pass_dB,Stop_dB);
% Results in a 5th Order filter with f_g = 0.1
[b,a] = cheby1(N,Pass_dB,f_g);
from scipy import signal
Pass_freq = 0.1
Pass_dB = 0.2
Stop_freq = 0.2
Stop_dB = 30
order, wn = signal.cheb1ord(wp=Pass_freq, ws=Stop_freq, gpass=Pass_dB, gstop=Stop_dB, fs=f_s)
[b, a] = signal.cheby1(N=order, rp=Pass_dB, Wn=Pass_freq, output='ba')
6.2.5.3. Tschebyscheff-II-Filter#
Das Tschebyscheff-II-Filter ist der Inverse Entwurf zum Typ I. Das Ziel ist also ein flacher Durchlassbereich und ein oszilierender Sperrbereich. Der dazugehörige Matlab-Code sieht folgendermaßen aus.
Pass_freq = 0.1; % Matlab uses normalized frequencies from 0..2
Pass_dB = 0.2;
Stop_freq = 0.2;
Stop_dB = 30;
[N,f_g] = cheb2ord(Pass_freq,Stop_freq,Pass_dB,Stop_dB);
% Results in a 5th Order filter with f_g = 0.2
[b,a] = cheby2(N,Stop_dB,f_g);
from scipy import signal
Pass_freq = 0.1
Pass_dB = 0.2
Stop_freq = 0.2
Stop_dB = 30
order, wn = signal.cheb2ord(wp=Pass_freq, ws=Stop_freq, gpass=Pass_dB, gstop=Stop_dB, fs=f_s)
[b, a] = signal.cheby2(N=order, rs=Stop_dB, Wn=Stop_freq, output='ba')
6.2.5.4. Cauer-Filter#
Das Cauer-Filter auch als Ellpitisches-Filter bezeichnet, definiert einen Equiripple-Entwurf im Durchlass- und Sperrbereich. Dies führt zu einer weiteren Reduzierung der Ordnung. Der Entwurf sieht wie folgt aus.
Pass_freq = 0.1; % Matlab uses normalized frequencies from 0..2
Pass_dB = 0.2;
Stop_freq = 0.2;
Stop_dB = 30;
[N,f_g] = ellipord(Pass_freq,Stop_freq,Pass_dB,Stop_dB);
% Results in a 4th Order filter with f_g = 0.1
[b,a] = ellip(N,Pass_dB,Stop_dB,f_g);
from scipy import signal
Pass_freq = 0.1
Pass_dB = 0.2
Stop_freq = 0.2
Stop_dB = 30
order, wn = signal.ellipord(wp=Pass_freq, ws=Stop_freq, gpass=Pass_dB, gstop=Stop_dB, fs=f_s)
[b, a] = signal.ellip(N=order, rp=Pass_dB, rs=Stop_dB, Wn=Pass_freq, output='ba')
6.2.5.5. Vor- und Nachteile der unterschiedlichen Entwurfsverfahren#
Die Wahl der Entwurfsmethode beruht im großen Maße auf den gegebenen Randparamtern. Um eine geeignete Wahl zu treffen ist es aber notwendig die Stärken und Schwächen der einzelnen Verfahren zu beleuchten. Aus den vorherigen Abschnitten ist bereits ersichtlich, dass die Ordnung der Filter und somit die Anzahl der benötigten Filterkoeffizienten vom Entwurf abhängt. Der Butterworth-Entwurf benötigt immer die größte Ordnung, während das Cauer-Filter immer mit der geringsten Ordnung auskommt. Gleichzeitig sind die resultierenden Koeffizienten auch für eine SOS-Lösung numerisch am fragilsten und benötigen eine hohe Quantisierung.
Um die weiteren Vor- und Nachteile zu verdeutlichen sind in Abbildung 6.19 die verschiedenen Entwurfsverfahren am oben verwendeten Beispiel gezeigt.
# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0 18.02.2022
#
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------
import matplotlib
import numpy
from scipy import signal
from matplotlib import pyplot
# determine where we're running from and set paths accordingly
try:
if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
prefix = ''
except:
prefix = '../../'
matplotlib.style.use(f'{prefix}sv.mplstyle')
fig, ((ax_durch_b_c1, ax_durch_c2_c), (ax_sperr_b_c1, ax_sperr_c2_c),
(ax_phase_b_c1, ax_phase_c2_c)) = pyplot.subplots(3, 2)
f_s = 48000
# filter design parameters
order = 4
Pass_freq = 0.1
Pass_dB = 0.2
Stop_freq = 0.2
Stop_dB = 30
# Filter design process:
# 1. find necessary order for the desired parameters
# 2. use corresponding filter design function,
# giving the necessary parameter (not always all of them)
# 3. calculate the transfer function using freqz on the filter coefficients
# displaying:
# 4. show amplitude of transfer function in Pass stop and transition,
# using fitting zooms
# 5. show phase. numpy.unwrap for smooth display i.e. no jumps from 2*pi to 0
# Butterworth vs Chebychev-1 filter design
# ----------------------------------------
# Butterworth:
order, wn = signal.buttord(wp=Pass_freq, ws=Stop_freq,
gpass=Pass_dB, gstop=Stop_dB)
[b, a] = signal.butter(N=order, Wn=Pass_freq, output='ba')
[w, h] = signal.freqz(b, a)
w = w/numpy.pi
ax_durch_b_c1.plot(w, 20*numpy.log10(numpy.abs(h)))
ax_durch_b_c1.set(xlabel='Frequenz in rad/s', ylabel='Pegel in dB',
xlim=[0, 0.15], ylim=[-1, 0.2], title='a) Durchlassbereich')
ax_sperr_b_c1.plot(w, 20*numpy.log10(numpy.abs(h)))
ax_sperr_b_c1.set(xlabel='Frequenz in rad/s', ylabel='Pegel in dB',
xlim=[0.1, 1], ylim=[-80, -20], title='b) Sperrbereich')
ax_phase_b_c1.plot(w, numpy.unwrap(p=numpy.angle(h)))
ax_phase_b_c1.set(xlabel='Frequenz in rad/s', ylabel='Phase in rad',
xlim=[0, 1], title='c) Phase')
# Cheby1
order, wn = signal.cheb1ord(wp=Pass_freq, ws=Stop_freq,
gpass=Pass_dB, gstop=Stop_dB, fs=f_s)
[b, a] = signal.cheby1(N=order, rp=Pass_dB, Wn=Pass_freq, output='ba')
[w, h] = signal.freqz(b, a)
w = w/numpy.pi
ax_durch_b_c1.plot(w, 20*numpy.log10(numpy.abs(h)), linestyle='--')
ax_sperr_b_c1.plot(w, 20*numpy.log10(numpy.abs(h)), linestyle='--')
ax_phase_b_c1.plot(w, numpy.unwrap(p=numpy.angle(h)), linestyle='--')
# Chebychev-2 vs Cauer filter design
# ----------------------------------
# Cheby2
order, wn = signal.cheb2ord(wp=Pass_freq, ws=Stop_freq,
gpass=Pass_dB, gstop=Stop_dB, fs=f_s)
[b, a] = signal.cheby2(N=order, rs=Stop_dB, Wn=Stop_freq, output='ba')
[w, h] = signal.freqz(b, a)
w = w/numpy.pi
ax_durch_c2_c.plot(w, 20*numpy.log10(numpy.abs(h)))
ax_durch_c2_c.set(xlabel='Frequenz in rad/s', ylabel='Pegel in dB',
xlim=[0, 0.15], ylim=[-1, 0.2], title='d) Durchlassbereich')
ax_sperr_c2_c.plot(w, 20*numpy.log10(numpy.abs(h)))
ax_sperr_c2_c.set(xlabel='Frequenz in rad/s', ylabel='Pegel in dB',
xlim=[0.1, 1], ylim=[-80, -20], title='e) Sperrbereich')
ax_phase_c2_c.plot(w, numpy.unwrap(p=numpy.angle(h)))
ax_phase_c2_c.set(xlabel='Frequenz in rad/s', ylabel='Phase in rad',
xlim=[0, 1], title='f) Phase')
# Cauer
order, wn = signal.ellipord(wp=Pass_freq, ws=Stop_freq,
gpass=Pass_dB, gstop=Stop_dB, fs=f_s)
[b, a] = signal.ellip(N=order, rp=Pass_dB, rs=Stop_dB,
Wn=Pass_freq, output='ba')
[w, h] = signal.freqz(b, a)
w = w/numpy.pi
ax_durch_c2_c.plot(w, 20*numpy.log10(numpy.abs(h)), linestyle='--')
ax_sperr_c2_c.plot(w, 20*numpy.log10(numpy.abs(h)), linestyle='--')
ax_phase_c2_c.plot(w, numpy.unwrap(p=numpy.angle(h)),linestyle='--')
pyplot.tight_layout()
pyplot.show()
# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("IIRDesign", fig, display=False)
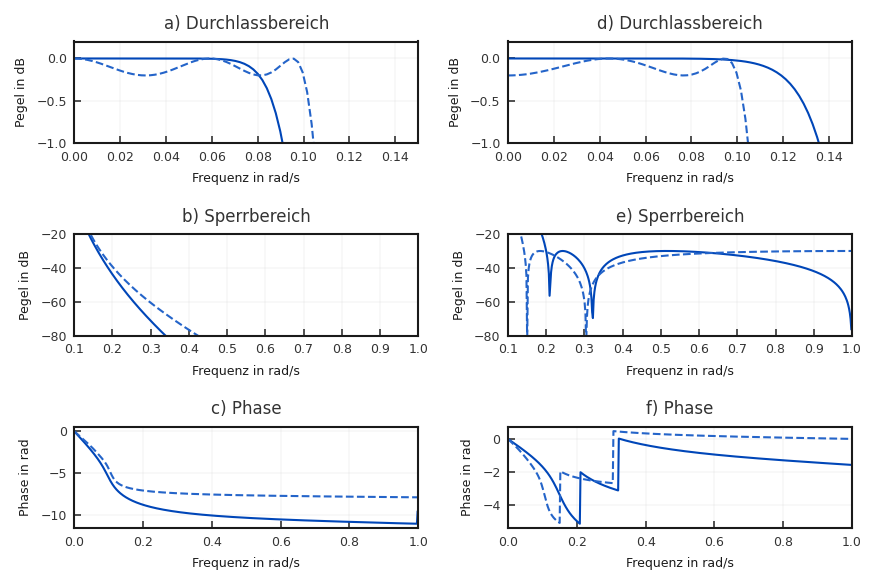
Fig. 6.19 Beispiel eines Tiefpass-Entwurfes für verschiedene Entwurfsverfahren.#
Das Butterworth-Filter hat im Durchlassbereich den erwarteten positiven flachen Verlauf, der im Sperrbereich zu einer monoton fallenden Dämpfung führt. Dieses Verhalten im Sperrbereich wird auch vom Tschebyscheff-I-Filter im Sperrbereich erreicht, wobei trotz der geringeren Ordnung ein zunächst steilerer Übergang an der Grenzfrequenz erreicht wird. Beim Tschebyscheff-II-Filter im Durchlassbereich wird deutlich, dass die Spezifikation übererfüllt wird. Die Grenzfrequenz bei der der Übergang beginnt, ist verschoben, da beim Tschebyscheff-II-Design in erster Linie der Sperrbereich erfüllt werden soll.
Ein bisher nicht beachteter Aspekt ist in den Bildern c und f gezeigt. Hier wird deutlich, dass die Phase im Übergangsbereich durch das Cauer-Filter am stärksten verzerrt wird, während das Butterworth-Filter am ehesten der meistens gewünschten linearen Phase entspricht.
To Do
Impuls bzw. Step-Verhalten zur Glättung
6.2.5.6. Entwurf von Hochpass, Bandpass und Bandsperr-Filter#
Bisher wurden nur Tiefpass-Entwürfe betrachtet. Alle anderen Filter lassen sich ebenfalls errechnen, wobei die dazu verwendeten Frequenz-Transformationen (nicht zu verwechseln mit der Fourier-Transformation) erst bei der Betrachtung der analogen Prototyp-Filter genauer erläutert werden soll.
Für den Entwurf mit Matlab ergibt sich für alle Verfahren das gleiche Schema. Ein Hochpass-Filter wird durch einen speziellen Schalter (Flag = “high”) angezeigt. Der Bandpass-Entwurf ergibt sich automatisch, wenn mehr als eine Grenzfrequenz angegeben wird, während die Bandsperre mit zwei Grenzfrequenzen und einem Flag = “stop” angezeigt wird. Zur Berechnung der Ordnung reicht es die Grenzfrequenzen zu vertauschen, um einen Hochpass anzuzeigen.
Beispiel:
% Highpass-Design
Pass_freq = 0.2; % Matlab uses normalized frequencies from 0..2
Pass_dB = 0.2;
Stop_freq = 0.1;
Stop_dB = 30;
[N,f_g] = buttord(Pass_freq,Stop_freq,Pass_dB,Stop_dB);
% Result is 7th Order and f_g = 0.1247
[b,a] = butter(N,f_g,'high');
%Bandpass Design
Pass_freqLow = 0.2; % Matlab uses normalized frequencies from 0..2
Pass_freqHigh = 0.3; % Matlab uses normalized frequencies from 0..2
Pass_dB = 0.2;
Stop_freqLow = 0.1;
Stop_freqHigh = 0.4;
Stop_dB = 30;
[N,f_g] = buttord([Pass_freqLow Pass_freqHigh],[Stop_freqLow Stop_freqHigh],Pass_dB,Stop_dB);
[b,a] = butter(N,f_g);
% Bandstop Design
Pass_freqLow = 0.1; % Matlab uses normalized frequencies from 0..2
Pass_freqHigh = 0.4; % Matlab uses normalized frequencies from 0..2
Pass_dB = 0.2;
Stop_freqLow = 0.2;
Stop_freqHigh = 0.3;
Stop_dB = 30;
[N,f_g] = buttord([Pass_freqLow Pass_freqHigh],[Stop_freqLow Stop_freqHigh],Pass_dB,Stop_dB);
[b,a] = butter(N,f_g,'stop');
# Highpass Design
Pass_freq = 0.2
Pass_dB = 0.2
Stop_freq = 0.1
Stop_dB = 30
order, wn = signal.buttord(wp=Pass_freq, ws=Stop_freq, gpass=Pass_dB, gstop=Stop_dB)
[b, a] = signal.butter(N=order, Wn=Pass_freq, btype='highpass', output='ba')
# Bandpass Design
Pass_freqLow = 0.2
Pass_freqHigh = 0.3
Pass_dB = 0.2
Stop_freqLow = 0.1
Stop_freqHigh = 0.4
Stop_dB = 30
order, wn = signal.buttord(wp=Pass_freq, ws=Stop_freq, gpass=Pass_dB, gstop=Stop_dB)
[b, a] = signal.butter(N=order, Wn=[Pass_freqLow, Pass_freqHigh], btype='bandpass', output='ba')
# Bandstop Design
Pass_freqLow = 0.1
Pass_freqHigh = 0.4
Pass_dB = 0.2
Stop_freqLow = 0.2
Stop_freqHigh = 0.3
Stop_dB = 30
order, wn = signal.buttord(wp=Pass_freq, ws=Stop_freq, gpass=Pass_dB, gstop=Stop_dB)
[b, a] = signal.butter(N=order, Wn=[Pass_freqLow, Pass_freqHigh], btype='bandstop', output='ba')
