4. z-Transformation#

Die z-Transformation stellt ein wichtiges Werkzeug zur Analyse und zum Verständnis von LTI-Systemen dar. Es werden durch die z-Systemfunktion und das Pol-Nullstellen-Diagramm neue Beschreibungsformen für LTI-Systeme aufgezeigt. Insbesondere wird eine Möglichkeit angegeben, um die Stabilität rekursiver LTI-Systeme zu testen.

4.1. Einführung#

Zunächst ein einfaches Beipiel, um die Nützlichlikeit der z-Transformation zu unterstreichen.

Angenommen auf ein Sparbuch wird ein bestimmter Geldbetrag \(S\) eingezahlt und dieser Betrag wird jährlich mit einem Zins \(p\) verzinst. Eine mathematische Darstellung dieses Sachverhalts ergibt sich durch Nutzung des Delta-Impulses gewichtet mit dem Geldbetrag und einer einfachen Rekursion, wobei ein leeres Konto als Startwert vorliegt. Es gilt also

(4.1)#\[ y(k) = (1+p) y(k-1) + S \delta(k) \]

mit \(y(k-1) = 0\). Dies ist eine andere Darstellung der Zinseszinsrechenregel

\[ \mbox{Geld} = S (1+p)^{\mbox{Jahre}}~~~. \]

Die Anzahl der Jahre ist in Formel (4.1) in der Anzahl der Rekursionen versteckt. Die zweite Form ist eine direkte Berechnung.

Nun lassen sich aber nicht für alle Rekursionssysteme solche einfachen direkten Rechenvorschriften angeben. Aber wie ist der mathematische Zusammenhang zwischen den beiden möglichen Lösungen?

In der Rekursionsformel

(4.2)#\[ y(k) = (1+p) y(k-1) + S \delta(k) \]

ergibt sich durch Variablensubstitution \(c = 1+p\)

(4.3)#\[ y(k) = c y(k-1) + S \delta(k)~~~. \]

Diese Form wird jetzt auf beiden Seiten mit der Summe \(\sum_{k = -\infty}^{\infty}z^{-k}\) multipliziert. Ein Schritt der mathematisch erlaubt ist, da er auf beiden Seiten des Gleichungssystems durchgeführt wird.

(4.4)#\[ \sum_{k = -\infty}^{\infty} y(k) z^{-k} = \underbrace{c \sum_{k = -\infty}^{\infty} y(k-1) z^{-k}}_{\mbox{1. Summand}} + \underbrace{S \sum_{k = -\infty}^{\infty} \delta(k) z^{-k}}_{\mbox{2. Summand}} \]

Mit Hilfe der abkürzenden Schreibweise

(4.5)#\[ Y(z) = \sum_{k = -\infty}^{\infty} y(k) z^{-k} \]

ergibt sich bei dem 2. Summanden für nur ein Element der Summe der Wert \(S\), da die \(\delta\)-Folge nur bei \(k = 0\) einen Wert ungleich Null hat.

Zusätzlich kann der 1. Summand durch eine Variablensubstitution \(k' = k-1\) umgeformt werden.

(4.6)#\[ c \sum_{k = -\infty}^{\infty} y(k-1) z^{-k} = c \sum_{k' = -\infty}^{\infty} y(k') z^{-k'-1} =c z^{-1}\sum_{k' = -\infty}^{\infty} y(k') z^{-k'}=c z^{-1} Y(z) \]

Somit ergibt sich

(4.7)#\[ Y(z) = c z^{-1} Y(z) + S~~~. \]

Umgestellt folgt

(4.8)#\[ Y(z) = \frac{S}{1-c z^{-1}}~~~. \]

Um zur Lösung für das Ausgangssignal zu kommen, wird die Summenformel für eine geometrische Reihe eingeführt.

(4.9)#\[ \sum_{k = 0}^{\infty} q^k = \frac{1}{1-q} \quad \mbox{wenn} \quad |q|<1 \]

Für Gleichung (4.8) ergibt sich also

(4.10)#\[ \frac{S}{1-c z^{-1}} = S \sum_{k = 0}^{\infty} (c z^{-1})^k = S \sum_{k = 0}^{\infty} c^k z^{-k}~~~. \]

Vergleicht man diese Lösung mit (4.5), ergibt sich

(4.11)#\[\begin{split} y(k) = \bigg\{ \begin{array}{lcc} S c^k & & k \geq 0\\ 0 & & k<0 \end{array} = S(1+p)^k \gamma(k)~~~, \end{split}\]

mit \(\gamma(k)\) als Sprungfolge (siehe Gleichung (2.11)).

Dies entspricht der vorher bekannten Lösung für die Zinseszinsformel.

4.2. Definition z-Transformation#

Für eine verkürzte Schreibweise wird für die z-Transformation folgendes Symbol eingeführt

(4.12)#\[ \mathcal{Z}\{ \cdot \}= \sum_{k = -\infty}^{\infty} (\cdot) z^{-k} \quad \text{mit} \quad z \in \mathbb{C}~~~. \]

Es gilt also

(4.13)#\[ Y(z) =\mathcal{Z}\{y(k)\}~~~. \]

Die Rechenvorschrift führt dazu, dass die diskrete Eingangsfolge \(y(k)\) auf eine komplexe Ebene abgebildet wird. Man spricht deshalb auch von Zeitbereichsdarstellung und Bildbereichdarstellung. Um die Korrespondenz zu symbolisieren wird häufig der sog. Transformationsknochen verwendet:

  • Hintransformation: \(y(k) \circ \hskip-1ex -\hskip-1.2ex -\hskip-1.2ex- \hskip-1ex \bullet\; Y(z)\) oder bei Gleichungsabfolgen vertikal,

  • Rücktransformation: \(Y(z) \bullet \hskip-1ex -\hskip-1.2ex -\hskip-1.2ex- \hskip-1ex \circ\; y(k)\).

Damit eine z-Transformation gültig ist, muss zusätzlich gelten, dass die Summe in Gl. (4.12) kleiner unendlich ist. Dies ist für alle endlichen Folgen gegeben, wenn keiner der Folgenwerte unendlich ist. Bei unendlichen Folgen ist dies nicht immer gewährleistet und hängt auch direkt von \(z\) ab. Deshalb gehört zu einer vollständigen Beschreibung der z-Transformation auch immer die Bereichsangabe von \(z\) in der die Summe konvergiert. Man spricht deshalb vom sogenannten Konvergenzgebiet Region of Convergence. Zur Beschreibung des Konvergenzgebietes reichen die Angaben der Radien \(r = |z|\) der komplexen Zahlen aus. Für das Konvergenzgebiet ergibt sich entweder das Gebiet inner- oder außerhalb einer Kreisfläche oder das Gebiet hat die Form eines Kreisringes in der z-Ebene.

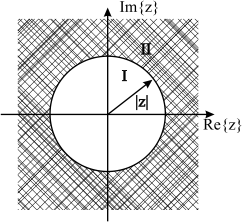
_images/ROC_Kausal.png

Fig. 4.1 Veranschaulichung des Konvergenzgebietes bei der z-Transformation. In diesem Beispiel für eine kausale Folge (ROC außerhalb).#

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

import matplotlib
import numpy
from matplotlib import pyplot

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

matplotlib.style.use(f'{prefix}sv.mplstyle')

index_kausal = numpy.linspace(-10, 10, 21)
amplitude_kausal = [0]*len(index_kausal)
mid_kausal = int(numpy.floor(len(index_kausal)/2))
for idx in range(len(index_kausal)-mid_kausal):
    amplitude_kausal[idx+mid_kausal] = 0.5**idx

fig, (ax_kausal, ax_nkausal) = pyplot.subplots(1, 2)
ax_kausal.stem(index_kausal, amplitude_kausal, use_line_collection=True)
ax_kausal.set(xlabel='Folgenkindex k ->', ylabel='Amplitude x(k)', title='kausale Folge 0.5**(k)*gamma(k)', xlim=[-10, 10])

index_nkausal = numpy.linspace(-10, 10, 21)
amplitude_nkausal = [0]*len(index_nkausal)
mid_nkausal = int(numpy.floor(len(index_nkausal)/2))
for idx in range(len(index_nkausal)-mid_nkausal):
    amplitude_nkausal[idx] = -1 * 0.5**(-10+idx)

ax_nkausal.stem(index_nkausal, amplitude_nkausal, use_line_collection=True)
ax_nkausal.set(xlabel='Folgenkindex k ->', ylabel='Amplitude x(k)', title='nicht kausale Folge -0.5**(-k)*gamma(-k)', xlim=[-10, 10], ylim=[-50, 0])

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("zFolgenPic", fig, display=False)

Beispiel

Betrachtet man die kausale Folge

(4.14)#\[\begin{split} \begin{aligned} x(k) &=& [0{,}5 \:\: 0{,}5^2 \:\: 0{,}5^3 \:\: \cdots \:\: 0{,}5^k]\\ & = & 0{,}5^k \gamma(k) \qquad~für~k \geq 0 ,\end{aligned} \end{split}\]

(siehe Abbildung 4.2 a), sie entspricht dem Sparbuchbeispiel mit einem Startkapital von 0{,}5 und 50 % Kontokosten, also einer ziemlich schlechten Geldanlage), so ergibt sich die z-Transformierte als

\[ X(z) = \sum_{k = -\infty}^{\infty} 0{,}5^k \gamma(k)z^{-k} = \sum_{k = 0}^{\infty} 0{,}5^k z^{-k} = \sum_{k = 0}^{\infty} (0{,}5z^{-1})^{k} \]

bzw. mit der Umformung durch die geometrische Reihe als

\[ X(z) = \frac{1}{1-0{,}5z^{-1}} = \frac{z}{z-0{,}5}~~~, \]

wobei das Konvergenzkriterium der geometrischen Reihe zusätzlich

\[ \nonumber |0{,}5z^{-1}| = \frac{0{,}5}{z} < 1 \qquad \Rightarrow \qquad |z| > 0{,}5 \]

fordert.

Definition:

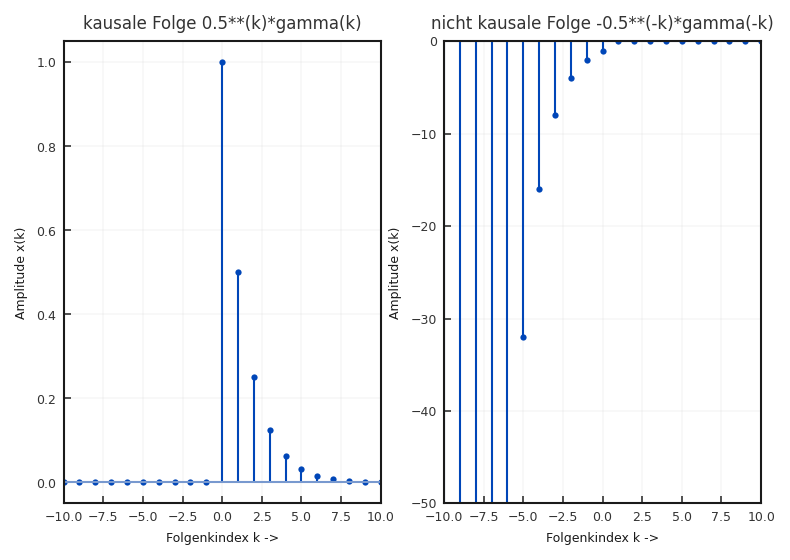
_images/ztrafo_2_1.png

Fig. 4.2 a) kausale Folge \(0{,}5^k \gamma(k)\) für \(k \geq 0\) und b) nicht-kausale Folge \(-0{,}5^k \gamma(-k-1)\) für \(k < 0\).#

Im folgenden soll nun eine sehr ähnlichen Folge, nämlich dem nicht-kausalen, negativen äquivalent zu (4.14)

\[ \nonumber x(k) = -0{,}5^k \gamma(-k-1) \qquad \text{für} \qquad k < 0 \]

betrachtet werden (siehe Abbildung 4.2 b). Berechnet man die z-Transformierte ergibt sich mit einer Variablensubstitution \(k = -m\)

\[\begin{split} \begin{aligned} \nonumber X(z) &=& - \sum_{k = -\infty}^{-1} 0{,}5^k z^{-k} \\ & = &- \sum_{k = -\infty}^{-1} (0{,}5^{-1}z)^{-k} \\ & = &- \sum_{m = 1}^{\infty} (0{,}5^{-1}z)^{m}\end{aligned} \end{split}\]

Nutzt man jetzt eine alternative Formulierung der unendlichen geometrischen Reihe

\[\nonumber \sum_{m = 1}^{\infty} x^m = \frac{x}{1-x} \]

so ergibt sich

\[ \nonumber X(z) = - \frac{0.5^{-1}z}{1-0{,}5^{-1}z} = \frac{z}{z-0{,}5}~~~. \]

Wir erhalten also die gleiche z-Transformation für unterschiedliche Folgen, wobei aber die Konvergenz der geometrischen Reihe für die anti-kausale Folge ein Konverzgebiet

\[\nonumber |z| < 0{,}5 \]

fordert. Abbildung 4.3 zeigt das dazugehörige Konvergenzgebiet in der z-Ebene. Man erkennt somit, warum eine Angabe des ROC bei der z-Transformation notwendig ist, um eine eindeutige Berechnung und Zuordnung zu gewährleisten.

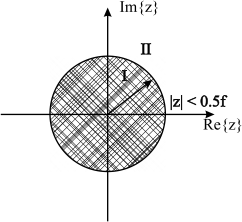
_images/ROC_AntiKausal.png

Fig. 4.3 Veranschaulichung des Konvergenzgebietes bei der z-Transformation. In diesem Beispiel für eine anti-kausale Folge (ROC innerhalb) mit \(|z| < 0{,}5\).#

4.3. Rechenregeln#

Die z-Transformation erleichtert das Rechnen von Differenzengleichungen. Einige häufig verwendete Rechenregeln und Korrespondenzen sind im Folgenden aufgeführt.

4.3.1. Linearität#

Die z-Transformation ist eine lineare Transformation. Es gilt

(4.15)#\[ a_1 x_1(k) + a_2 x_2(k) ;\circ \hskip-1ex -\hskip-1.2ex -\hskip-1.2ex- \hskip-1ex \bullet\; a_1 X_1(z) + a_2 X_2(z)~~~. \]

4.3.2. Verschiebung#

Die zeitliche Verschiebung der diskreten Folge wurde bereits in den Beispielen ausgiebig verwendet. Es gilt:

(4.16)#\[ \mathcal{Z}\{y(k-k_0)\} = z^{-k_0} Y(z) \]

4.4. Rück-Transformation#

Die z-Transformation transformiert eine diskrete Folge in eine kontinuierliche komplexe Ebene. In den Beispielen wurde für die Rücktransformation in den Zeitbereich stets mit einfachen gebrochen rationalen Funktionen gearbeitet, die direkt auf eine bestimmte Folge führten. Dies ist nicht immer möglich. Die allgemeinste Version der z-Rücktransformation ist durch das Umlaufintegral

(4.17)#\[ x(k) = \oint_C X(z) z^{k-1} \text{d}z \]

gegeben. Dies bedeutet wir umlaufen die komplexe Ebene auf dem Kreis C im mathematisch positiven Sinn (Gegenuhrzeigersinn) und integrieren die eingeschlossene Fläche. Dies ist nicht immer möglich. Ob die Möglichkeit besteht hängt direkt davon ab, wie das Konvergenzgebiet definiert ist. Auf die explizite Behandlung der Thematik wird hier nicht eingegangen, statt dessen wird auf [OS99] verwiesen.

In vielen Fällen kann auf die Lösung des Integrals verzichtet werden. Statt dessen sind häufig Lösungen über Partialbruchzerlegung (siehe Beispiele) und/oder Korrespondenztabellen möglich

4.4.1. Korrespondenztabelle#

Viele Systeme und Signale lassen sich auf einfache Grundformen zurückführen. Für diese Grundformen kann für die Hin- und Rücktransformation Tabelle 4.1 verwendet werden.

Table 4.1 Korrespondenztabelle#

Zeitbereich \(y(k)\)

Bildbereich \(Y(z) = \mathcal{Z}\{y(k)\}\)

Konvergenzgebiet

\(\delta(k)\)

1

\(\forall z\)

\(\gamma{k}\)

\(\frac{z}{z-1} = \frac{1}{1-z^{-1}}\)

\(\text{abs(z)}>1\)

\(k \gamma(k)\)

\(\frac{z}{(z-1)^2}\)

\(\text{abs(z)}>1\)

\(e^{-\alpha k}\gamma (k)\)

\(\frac{z}{z-e^{-\alpha}}\)

\(\text{abs(z)}>e^{-\alpha}\)

\(\alpha^k \gamma (k)\)

\(\frac{z}{z-\alpha}\)

\(\text{abs(z)} > \alpha\)

\(\cos(\omega_0 k)\)

\(\frac{1-z^{-1} \cos(\omega_0)}{1-z^{-1} 2\cos(\omega_0)+z^{-2}}\)

\(\text{abs(z)}>1\)

Eine Beschreibung von LTI-Systemen kann wie im letzten Abschnitt gezeigt über Differenzengleichungen erfolgen. Die z-Transformation und Rücktransformation solcher Systeme sind besonders gut über die Korrespondenztabellen zu lösen.

Beispiel: LTI-System

Wie lautet die z-Transformierte für die Differenzengleichung

\[ y(k) = 0{,}2y(k-1) - y(k-3) + x(k) + 1{,}2x(k-1) - 3{,}2 x(k-2)~~~\text{?} \]

Entscheidend ist, dass nur einfache Verzögerungen \(k_0\) auftreten, die in der z-Ebene durch \(z^{-k_0}\) dargestellt werden. Es ergibt sich mit der Eigenschaft der Linearität

\[ Y(z) = 0{,}2Y(z) z^{-1} - Y(z) z^{-3} + X(z) + 1{,}2X(z) z^{-1} - 3{,}2X(z) z^{-2}~~~. \]

4.5. Systemfunktion#

Bei den zur Einführung verwendeten Beispielen wurden sehr einfache Eingangsfolgen für \(x(k)\) verwendet. Man könnte das Sparbuch-Beispiel aber auch erweitern und annehmen, dass pro Jahr eine nicht näher definierte Summe zusätzlich auf das Konto eingezahlt wird. Die rekursive Formulierung für den Ausgang latet dann

(4.18)#\[ y(k) = (1+p) y(k-1) + x(k) ~~~. \]

Eine Transformation mit der Definition (4.12) in den z-Bereich führt zu

(4.19)#\[ Y(z) = (1+p)z^{-1} Y(z) + X(z)~~~. \]

Dies ergibt umgeformt

(4.20)#\[ Y(z) = \frac{X(z)}{1-(1+p)z^{-1}}~~~. \]

Teilt man diese Lösung durch \(X(z)\) ergibt sich auf der rechten Seite der Gleichung der Anteil, der unabhängig vom Eingangssignal ist und nur das System repräsentiert. Der Bruch \(Y(z)/X(z)\) wird zusätzlich durch mit \(H(z)\) abgekürzt.

(4.21)#\[ H(z) = \frac{Y(z)}{X(z)} = \frac{1}{1-(1+p)z^{-1}} \]

Die Funktion \(H(z)\) wird z-Systemfunktion genannt und beschreibt ein LTI-System vollständig. Eine andere vollständige Beschreibung eines LTI-Systems unabhängig vom Eingangssignal war die Impulsantwort \(h(k)\) eines Systems. Beide Darstellungsarten sind durch die z-Transformation miteinander verbunden. Es gilt

(4.22)#\[ \mathcal{Z}\{h(k)\} = H(z)~~~. \]

Wichtig

Die z-Transformation der Impulsantwort h(k) ist die Systemfunktion H(z).

Beispiel: z-Übertragungsfunktion

Die z-Transformierte aus dem vorherigen Beispiel war gegeben durch

\[ Y(z) = 0{,}2Y(z) z^{-1} - Y(z) z^{-3} + X(z) + 1{,}2X(z) z^{-1} - 3{,}2X(z) z^{-2} \]

die z-Systemfunktion ergibt sich durch wenige Umformungsschritte

\[\begin{split} \begin{aligned} \nonumber Y(z)- 0{,}2Y(z) z^{-1} + Y(z) z^{-3} & = & X(z) + 1{,}2X(z) z^{-1} - 3{,}2X(z) z^{-2}\\\nonumber Y(z) \left(1-0{,}2z^{-1} + z^{-3} \right) &=& X(z) \left(1 +1{,}2z^{-1} - 3{,}2 z^{-2} \right)\\ H(z) = \frac{Y(z)}{X(z)} &= & \frac{1 +1{,}2z^{-1} - 3{,}2 z^{-2}}{1-0{,}2z^{-1} + z^{-3}}\end{aligned} \end{split}\]

Die Verknüpfung von \(h(k)\) und dem Eingangssignal \(x(k)\) zum Ausgangssignal \(y(k)\) erfolgt im Zeitbereich über die Faltung. Bei der z-Systemfunktion ist die Verknüpfung von Eingang und Ausgang durch die Multiplikation gegeben. Es gilt also

(4.23)#\[ \mathcal{Z}\{a(k)\ast b(k)\} = A(z) B(z)~~~. \]

Damit haben wir eine Möglichkeit gefunden die eher aufwendige Faltungsumme mit Hilfe der z-Transformation in eine einfache Multiplikation im z-Bereich zu überführen. Das Ausgangssignal erhält man abschließend durch die inverse z-Transformation des Ausgangssignals \(Y(z)\). Dieser Lösungsweg ist in Abbildung 4.4 schematisch dargestellt.

_images/SchematischezLoesungFaltung.png

Fig. 4.4 Schematische Darstellung zur Berechnung der Faltungssumme mit Hilfe der z-Transformation.#

Beispiel

Ein System ist durch

\[ y(k) = x(k) -2x(k-1) + x(k-2) \]

gegeben. Die z-Transformation führt auf eine z-Systemfunktion

\[ H(z) = 1-2z^{-1} + z^{-2}~~~. \]

Für die Eingangsfolge:

\[ x(k) = \delta(k) + 2\delta(k-1) + 3\delta(k-2) + 4\delta(k-3) + 5\delta(k-4) \]

ergibt sich die z-Transformierte zu

\[ X(z) = 1 + 2z^{-1} + 3z^{-2}+ 4z^{-3}+ 5z^{-4}~~~. \]

Eine Polynommultiplikation führt zu der Ausgangs-z-Funktion

\[ Y(z) = X(z)H(z) = 1 -6 z^{-5} + 5 z^{-6}~~~. \]

Damit ergibt sich für die Ausgangsfolge

\[ y(k) = [1 \:\: 0 \:\: 0 \:\: 0 \:\: 0 \:\: -6 \:\: 5] \]

bzw.

\[ y(k) = \delta(k) - 6 \delta(k-5) + 5 \delta(k-6)~~~. \]

Wichtig

Die Faltung wird in der z-Ebene zu einer Multiplikation.

4.6. Pol-Nullstellenplan#

Nachdem die Äquivalenz der Impulsantwort mit der z-Systemfunktion \(H(z)\) bekannt ist, ist es möglich, Systeme besser zu analysieren. Dazu schauen wir zunächst auf die typische Systemfunktion

(4.24)#\[ H(z) = \frac{b_0 + b_1z^{-1} + b_2z^{-2}+ \cdots b_M z^{-M} }{1 + a_1z^{-1} + a_2z^{-2}+ \cdots a_N z^{-N}} = \frac{\displaystyle \sum_{i=0}^M b_iz^{-i}} {\displaystyle \sum_{i=0}^N a_i z^{-i}} \quad \text{mit} \quad~a_0 = 1 ~~~. \]

Unter der Annahme, dass der Zählergrad \(M\) kleiner oder gleich dem Nennergrad \(N\) ist, handelt es sich um ein kausales System 1. Die Ordnung des Systems wird unter dieser Annahme durch \(N\) angegeben. Im allgemeinen Fall definiert das Maximum von \(N\) und \(M\) die Ordnung des Systems.

Die gebrochen rationale Funktion kann auch in der äquivalenten Produktform geschrieben werden, wenn alle Nullstellen des Zähler- und Nennerpolynoms bekannt sind. Die Nullstellen des Nenners bezeichnet man als Polstellen bzw. Pol, da an diesen Punkten, die Übertragungsfunktion unendlich wird.

(4.25)#\[\begin{split} \begin{aligned} H(z) & = & b_0 \frac{(z-n_0)(z-n_1)\cdots(z-n_{M-1})}{(z-p_0)(z-p_1)\cdots(z-p_{N-1})}\\ & = & b_0 \frac{\displaystyle \prod_{i = 0}^{M-1}(z-n_i)} {\displaystyle \prod_{i = 0}^{N-1}(z-p_i)} \end{aligned} \end{split}\]

Für reelle Koeffizienten \(b_i\) und \(a_i\) ergeben sich dabei immer nur reelle Nullstellen oder konjugiert komplexe Paare.

Beispiel

\[\begin{split} \begin{aligned} \nonumber H(z) & = & \frac{3+6z^{-1}+3z^{-2}}{1{,}0000 -1{,}7119 z^{-1} + 0{,}8100 z^{-2}}\\\nonumber &=& 3\frac{(z+1)(z+1)}{(z-0{,}8560 - 0{,}2781j)(z-0{,}8560 + 0{,}2781j)}\\\nonumber &=& 3\frac{(z+1)^2}{(z-0{,}9e^{j\frac{\pi}{10}})(z-0{,}9e^{-j\frac{\pi}{10}})}\end{aligned} \end{split}\]

Um bestimmte Eigenschaften zu verdeutlichen ist es oft sinnvoll, die Pole und Nullstellen in der komplexen Ebene einzuzeichnen. Dabei werden Nullstellen durch ein o und Pole durch ein x markiert. Für das Beispiel ergibt sich der folgende Pol-Nullstellenplan, wobei ein eventuell vorhandener Skalierungsfaktor \(b_0\) nicht berücksichtige wird. Der Pol- Nullstellenplan ohne die Angabe von \(b_0\) ist deshalb keine vollständige Beschreibung eines LTI-Systems.

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

# based on https://matplotlib.org/3.1.0/gallery/mplot3d/surface3d_radial.html 

"""
Dem Polnullstellenplan kann per Rechtsklick eine Nullstelle, und per Linksklick eine Pollstelle hinzugefügt werden. Um eine Pol- / Nullstelle zu löschen muss man während man auf sie klickt 'Strg' halten. Es werden automatisch die konjugierten Pol- / Nullstellen hinzugefügt und gelöscht
"""

from mpl_toolkits.mplot3d import Axes3D
import numpy
import matplotlib
from matplotlib import pyplot
from matplotlib import cm

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

matplotlib.style.use(f'{prefix}sv.mplstyle')

def H_from_pole_zero(C):
    zaehler = numpy.ones_like(C)
    nenner = numpy.ones_like(C)

    for idx in range(len(zeros)):
        null = numpy.multiply(C - zeros[idx], C - numpy.conjugate(zeros[idx]))
        zaehler = numpy.multiply(zaehler, null)
        
    for idx in range(len(poles)):
        pole = numpy.multiply(C - poles[idx], C - numpy.conjugate(poles[idx]))
        nenner = numpy.multiply(nenner, pole)

    H = zaehler/(nenner+0.0000001)
    Z = 20*numpy.log10(numpy.abs(H))
    max_val = 60
    Z[Z>max_val]=max_val
    Z[Z<-max_val] = -max_val
    return Z

# Create the mesh in polar coordinates and compute corresponding Z.
theta = numpy.linspace(0, 2*numpy.pi, 100)
circle = numpy.exp(1j*theta)

x = numpy.linspace(-1.5, 1.5, 100)
y = numpy.linspace(-1.5j, 1.5j, 100)

poles = [0.8560 + 0.2781j]
zeros = [-1+0j]
#poles_conj = [0]*2
#zeros_conj = [0]*2
fig = pyplot.figure()
ax_pz = fig.add_subplot(121)

ax_pz.plot(circle.real, circle.imag)
ax_pz.set(xlabel=r'Realteil', ylabel=r'Imaginärteil', 
          title='Pol-Nullstellen-Plan', xlim=[-1.5, 1.5], ylim=[-1.5, 1.5])
ax_pz.axis('equal')

for idx in range(len(poles)):
    ax_pz.plot([poles[idx].real, poles[idx].real], [poles[idx].imag, -poles[idx].imag], marker='X', linestyle='none', color='red')
    ax_pz.plot([zeros[idx].real, zeros[idx].real], [zeros[idx].imag, -zeros[idx].imag], marker='o', linestyle='none', color='blue')

ax_pz.text(-0.95,-0.1,"2", color = 'blue', fontsize = 7)


X, Y = numpy.meshgrid(x, y)
C = X + Y

Z = H_from_pole_zero(C)

Y = Y.imag

ax_3d = fig.add_subplot(122, projection='3d')
ax_3d.plot_surface(X,Y,Z, cmap=cm.coolwarm, alpha=0.8)
X_c = circle.real
Y_c = circle.imag
Z_c = H_from_pole_zero(circle)

ax_3d.plot(X_c, Y_c, Z_c, color='black')

ax_3d.set(xlim=[-1.5, 1.5], ylim=[-1.5, 1.5], zlim=[-60, 60])
ax_3d.set_xlabel('Realteil')
ax_3d.set_ylabel('Imaginärteil')
ax_3d.set_zlabel(r'$H$ in dB')

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("PolNullstellenplan", fig, display=False)
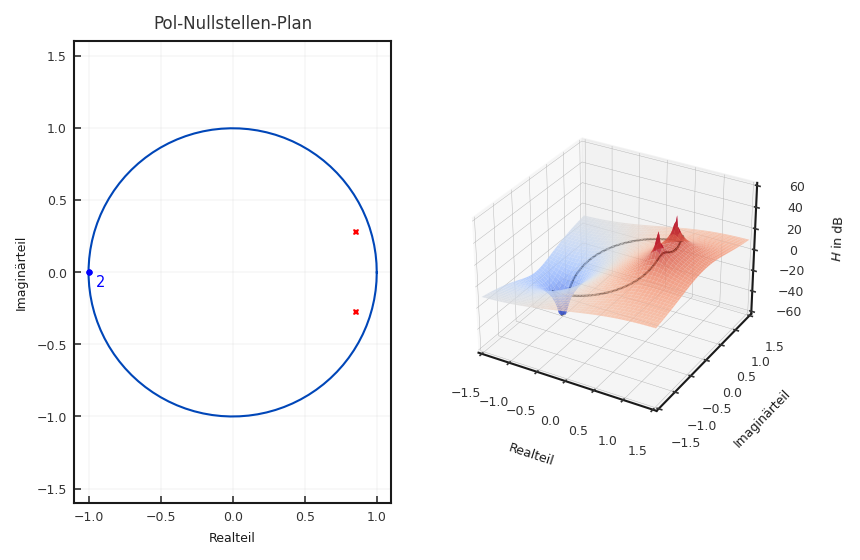
_images/ztrafo_10_1.png

Fig. 4.5 Pole und Nullstellen in der komplexen Ebene.#

  1. Starten des interaktiven Programms - ZTrafo_Pol_Null_3D.py in jupyterbook/code/interactive_programs/

  2. Eigene Pole und Nullstellen per Klick definieren bzw. löschen (zusätzlich STRG halten):

    • Rechtsklick: Nullstelle

    • Linksklick: Polstelle

Mehrfachnullstellen (oder auch Pole) werden durch eine zusätzliche Zahl gekennzeichnet, hier die zwei für die doppelte Nullstelle bei \(z = -1\). Weiterhin ist der sog. Einheitskreis zu sehen, der den Radius eins markiert und eine besondere Bedeutung hat.

Zur Verdeutlichung der Auswirkungen von Polen und Nullstellen in der komplexen Ebene ist auf der rechten Seite in Abbildung 4.5 der Betrag der Übertragungsfunktion in Abhängigkeit vom Real und Imaginärteil für das eben verwendete Beispiel gezeigt (die Darstellung erfolgt logarithmisch). Zur Orientierung ist zusätzlich der Einheitskreis eingezeichnet.

Der Einfluss der beiden Extremstellen auf den Betrag der Übertragungsfunktion ist auf der ganzen z-Ebene sichtbar. Man erkennt sehr deutlich, wie die Pole zu einem unendlichen Betrag führen, während die doppelte Nullstelle den Betrag zu Null (\(-\infty\) in dB) werden lässt.

Welche Auswirkungen haben nun Polstellen auf die Systemeigenschaften und insbesondere auf das Verhalten im Zeitbereich? Grundsätzlich lassen sich die komplexen Pole immer auch in der Polarschreibweise (Radius und Phase) angeben.

Ausgehend von einem System mit nur einem Pol (komplexwertiges System)

(4.26)#\[ H(z) = \frac{1}{1-re^{j\varphi}z^{-1}} \]

ergibt sich bei der Rücktransformation (Nutzung der Korrespondenztabelle) in den Zeitbereich

(4.27)#\[ h(k) = \gamma(k) r^k e^{j\varphi k}~~~. \]

Interpretiert man Gleichung (4.27) so ist zu erkennen, dass die Impulsantwort aus einer komplexen Schwingung (\(e^{j\varphi k}\)) und einem Faktor besteht, der die Amplitude ändert. Dieser Amplitudenfaktor wird als Einhüllende der komplexen Schwingung bezeichnet. Die Frequenz der Schwingung ist durch den Polwinkel \(\varphi\) definiert und die Form der Einhüllenden durch den Radius \(r\). Für \(r<1\) ergibt sich eine gedämpfte Exponentialfunktion. Bei \(r=1\) ist die komplexe Schwingung ungedämpft und bei \(r>1\) handelt es sich um eine aufklingende, also mit der Zeit stärker werdende Schwingung.

Dies ist in der Abbildung 4.6 nochmals verdeutlicht. Die Pollage a) ist ein Pol auf der reellen Achse mit einem Radius von \(r = 0{,}96\) (die eingezeichneten Pollagen sind zur Verdeutlichung skaliert). Die dazugehörige Schwingung ist eine abklingende Exponentialfunktion ohne Schwingungsanteil. Ist der Radius größer eins (b) \(r= 1{,}01\)) ergibt sich eine aufklingende Exponentialfunktion. Verschiebt man den Pol auf dem Radius \(r=0{,}96\) auf einen Polwinkel \(\varphi = \pi/10\), so ergibt sich eine exponentiell abklingende Schwingung (siehe c)). Bei einem Radius größer eins, eine aufklingende Schwingung (d). Die Drehung ist bei \(\varphi = 3\pi / 4\) kaum noch zu erkennen (e), während die Frequenz \(\varphi = \pi\) erneut zu einer reellen Folge mit wechselndem Vorzeichen führt. Der Radius entscheidet über das Abklingverhalten (g,f). Die Drehrichtung wird durch die Pollage in der oberen oder unteren Halbebene angegeben.

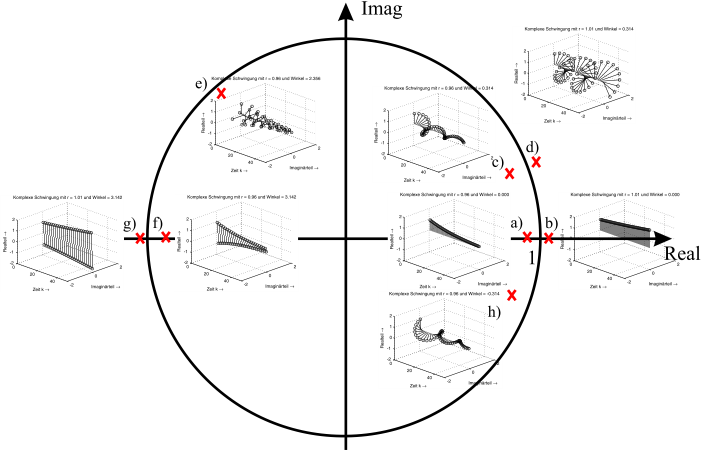
_images/PolLagen.png

Fig. 4.6 Mögliche Pollagen und die dazugehörigen komplexen Schwingungen im Zeitbereich (angelehnt an [GRS13]).#

Bei konjugiert komplexen Polpaaren heben sich durch die gegensinnigen Drehrichtungen die Imaginäranteile auf und die Impulsantwort \(h(k)\) ist rein reellwertig. Die ausgebildeten Schwingungen entsprechen gedämpften oder aufklingenden Cosinusfunktionen der Frequenz \(\varphi\).

Für konjugiert (\(^{\ast}\)) komplexe Polpaare gilt

\[ \frac{Az}{z-a} + \frac{A^{\ast}z}{z-a^{\ast}} ;\bullet \hskip-1ex -\hskip-1.2ex -\hskip-1.2ex- \hskip-1ex \circ\; 2|A||a|^k\cos(\arg\{a\}k + \arg\{A\})\gamma(k) ~~~, \]

wobei \(\arg\{x\}\) das Argument (der Winkel) der komplexen Zahl \(x\) ist.

Beispiel

Ausgehend von dem System

\[ H(z) = \frac{z^2}{(z-0{,}9e^{j\frac{\pi}{10}})(z-0{,}9e^{-j\frac{\pi}{10}})} \]

ergibt sich für die Aufspaltung

\[ H(z) = \frac{Az}{z-0{,}9e^{j\frac{\pi}{10}}} + \frac{A^{\ast}z}{z-0{,}9e^{-j\frac{\pi}{10}}} \]

mit

\[\begin{split} \begin{aligned} A &=& (z-0{,}9e^{j\frac{\pi}{10}})\widetilde{H}(z)\Bigg|_{z = 0{,}9e^{j\frac{\pi}{10}}}\\ & = & \frac{z}{z-0{,}9e^{-j\frac{\pi}{10}}}\Bigg|_{z = 0{,}9e^{j\frac{\pi}{10}}}\\ & = & \frac{0{,}9e^{j\frac{\pi}{10}}}{0{,}9e^{j\frac{\pi}{10}}-0{,}9e^{-j\frac{\pi}{10}}}\\ & = & -j\frac{e^{j\frac{\pi}{10}}}{2\sin \frac{\pi}{10}}\end{aligned} \end{split}\]

Die Impulsantwort ist also durch

\[ h(k) = 2\cdot 1{,}618 \cdot 0{,}9^k \cos\biggl(\frac{\pi}{10}k +\left(-\frac{\pi}{2} + \frac{\pi}{10}\right)\biggr)\gamma(k) \]

gegeben und wird in Abbildung 4.7 bis \(k = 49\) gezeigt.

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

import matplotlib
import numpy
from matplotlib import pyplot

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

matplotlib.style.use(f'{prefix}sv.mplstyle')

def impulse(num_samples, pole):
    r_pole = (pole.real**2 + pole.imag**2)**0.5 
    phi_pole = numpy.angle(pole) # in rad/s
    A = -1j*(numpy.exp(1j*phi_pole))/(2*numpy.sin(phi_pole))
    r_A = numpy.abs(A)
    phi_A = numpy.angle(A)
    y = numpy.zeros(num_samples)
    for idx in range(num_samples):
        y[idx] = 2 * r_A * r_pole**idx * numpy.cos(phi_pole*idx + phi_A)
    return y

def onclick(event):
    ax_pz.lines[1].remove()
    ax_imp.cla()

    pole = event.xdata + 1j*event.ydata
    y = impulse(50, pole)
    
    ax_pz.plot([pole.real, pole.real], [pole.imag, -pole.imag], marker='X', linestyle='none', color='blue')
    ax_imp.stem(y, use_line_collection=True)
    ax_imp.set(xlabel='Folgenkindex k ->', ylabel='Amplitude', title=f'Impulsantwort des Systems', xlim=[0, num_samples-1], ylim=[-y.max(), y.max()])
    fig.canvas.draw_idle()



theta = numpy.linspace(0, 2*numpy.pi, 100)
circle = numpy.exp(1j*theta)
pole = 0.8560 + 0.2781j

fig, (ax_pz, ax_imp)= pyplot.subplots(1, 2)

# Pole-Zero Plot
ax_pz.axis('equal')
ax_pz.set(xlabel=r'Realteil', ylabel=r'Imaginärteil', title='Pol-Nullstellen-Plan', xlim=[-1.5, 1.5], ylim=[-1.5, 1.5])
ax_pz.plot(circle.real, circle.imag)
ax_pz.plot([pole.real, pole.real], [pole.imag, -pole.imag], marker='X', linestyle='none', color='blue')

num_samples = 50
y = impulse(num_samples, pole)


# Impulse Plot
ax_imp.stem(y, use_line_collection=True)
ax_imp.set(xlabel=r'Folgenkindex $k \rightarrow$ ', ylabel='Amplitude', title='Impulsantwort des Systems', xlim=[0, num_samples-1])

cid = fig.canvas.mpl_connect('button_press_event', onclick)

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("BspKonjKomplexPole", fig, display=False)
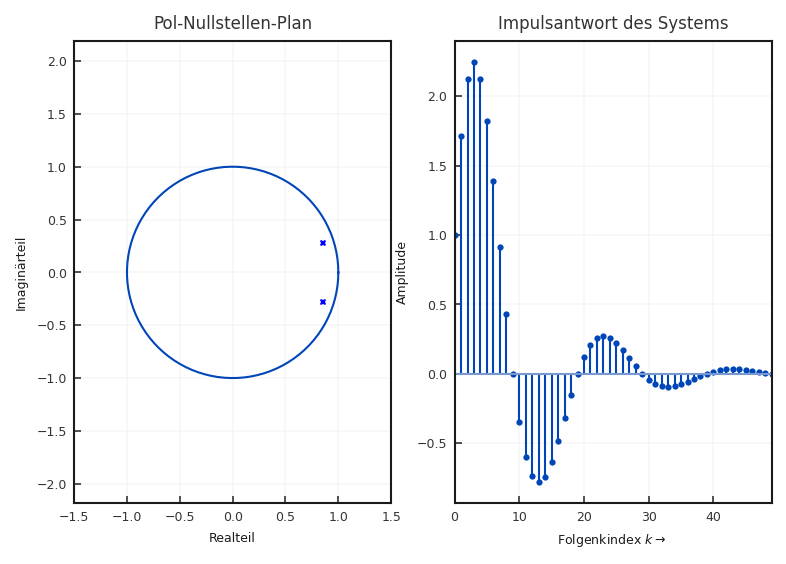
_images/ztrafo_17_1.png

Fig. 4.7 Beispiel der Impulsantwort eines Systems mit konjugiert komplexen Polpaar.#

  1. Starten des interaktiven Programms - ZTrafo_Pol_Null_Impulsantwort.py in jupyterbook/code/interactive_programs/

  2. Per Linksklick neue Polstelle definieren

4.7. Stabilität#

Mit den Erklärungen für Abbildung 4.6 ist die Frage nach einem Stabilitätstest für kausale LTI-Systeme recht einfach zu beantworten. Da alle Systeme mit Polradien größer eins aufklingende Schwingungen erzeugen sind die dazugehörigen Impulsantworten nicht endlich. Auf einen endlichen Impuls reagiert das System mit einer unendlichen Ausgangsgröße. Damit ist die BIBO-Bedingung nicht mehr erfüllt.

Wichtig

Stabile, kausale Systeme haben nur Pole innerhalb des Einheitkreises.

Wichtig

Quasistabil sind Systeme mit einfachen Polen auf dem Einheitskreis.

Allgemein lässt sich sagen, dass Systeme deren z-Konvergenzgebiet den Einheitskreis mit einschließen, stabil sind. Betrachtet man noch einmal die Beispiele für z-Transformation und des dazugehörigen Konvergenzgebietes in Abschnitt 4.2, so wird deutlich, dass die kausale Folge ein stabiles System darstellt, während die nicht-kausale Folge instabil ist. Man kann dies auch daran erkennen, dass die Folge mit wachsendem \(k\) größer wird.

Für LTI-Systeme ergibt sich als Kriterium für die BIBO-Stabilität

(4.28)#\[ \int_{-\infty}^{\infty} |h(t)|^2 dt < \infty~~~, \]

für diskrete Systeme gilt

(4.29)#\[ \sum_{k = -\infty}^{\infty}|h(k)|^2 < \infty~~~. \]

4.7.1. Stabilität eines Systems 2. Ordnung#

Systeme zweiter Ordnung sind in der digitalen Signalverarbeitung ein wichtiger Grundbaustein. Es ist deshalb interessant allgemein die Stabilitätsbedingungen zu berechnen. Das System ist durch

\[ H(z)=\frac{1}{1+a_{1}z^{-1}+a_{2}z^{-2}} \]

gegeben. Um die Polstellen des Polynoms zu berechnen, muss

\[ z^{2}+a_{1}z+a_{2}=0 \]

mit der bekannten pq-Formel

\[\begin{split} \begin{aligned} z_{1}& = &-\frac{a_{1}}{2}+\sqrt{\frac{a_{1}^{2}}{4}-a_{2}}\\ z_{2}& = &-\frac{a_{1}}{2}-\sqrt{\frac{a_{1}^{2}}{4}-a_{2}}\end{aligned} \end{split}\]

berechnet werden.

Die Stabilität ist immer für einen Betrag von \(\left|z\right|<1\) gesichert. Welche Bedingungen müssen für die Koeffizienten \(a_1\) und \(a_2\) gelten?

Zur Lösung nehmen wir zunächst eine Fallunterscheidung vor:

  1. Für die komplexwertige Lösung \(a_{2}>\frac{a_{1}^{2}}{4}\) ergibt sich durch die Nebenbedingung, dass man \(\sqrt{-1} = j\) vor die Wurzel ziehen kann und sich somit die Vorzeichen umdrehen. \(z=-\frac{a_{1}}{2} \pm j \sqrt{a_{2}-\frac{a_{1}^{2}}{4}}\)~~~.

Berechnet man den Betrag so ergibt sich

\[\begin{split} \begin{aligned} \left|z\right| & = & \sqrt{\frac{a_{1}^{2}}{4}+a_{2}-\frac{a_{1}^{2}}{4}}\\ & = & \sqrt{a_{2}} ~~~. \end{aligned} \end{split}\]

Da für ein stabiles System \(\left|z\right|<1\) gelten muss, gilt als erste Bedingung, dass auch \(a^2_{2}<1\) sein muss

  1. Für die reelwertige Lösung gilt \(a_{2}<\frac{a_{1}^{2}}{4}\):
    Es ergibt sich damit die Ungleichung

    \[ -1 < -\frac{a_{1}}{2} \pm \underbrace{\sqrt{\frac{a_{1}^{2}}{4}-a_{2}}}_{>0} < 1~~~. \]

    Löst man diese Ungleichung zunächst für das erste Ungleichheitszeichen und nutzt die negative Lösung, da diese ja immer kleiner ist als die positive Lösung

    \[ -1<-\frac{a_{1}}{2} - \sqrt{\frac{a_{1}^{2}}{4}-a_{2}} \]

    ergibt sich (zunächst Multiplikation mit -1, danach quadrieren und ausrechnen)

    \[\begin{split} \begin{aligned} -1+\frac{a_{1}}{2} & < & - \sqrt{\frac{a_{1}^{2}}{4}-a_{2}}\\ \left(1-\frac{a_{1}}{2}\right)^{2}& > & \frac{a_{1}^{2}}{4}-a_{2}\\ 1-2\frac{a_{1}}{2}+\frac{a_{1}^{2}}{4}& > & \frac{a_{1}^{2}}{4}-a_{2}\\ 1-a_1 & > & -a_2 \\ a_{1} & < & a_{2}+1 \end{aligned} \end{split}\]

    Für das zweite Ungleichheitszeichen gilt Entsprechendes. Die zweite Bedingung lautet

    (4.30)#\[ a_1 > -a_2 -1~~~. \]

Fasst man diese Bedingungen zusammen, ergibt sich für \(a_2\) eine untere Grenze von \(a_2>-1\). Alles zusammen beschreibt ein Dreieck, dass als Stabilitätsdreieck für kausale Systeme 2. Ordnung bezeichnet wird (siehe Abbildung 4.8).

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

# This script creates an interactive graphic, where the user can set a1 and a2 coeffitients by clicking a point in left graph. The right graph will show the corresponding impulse response of the defined system

import matplotlib
import numpy 
from matplotlib import pyplot

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

matplotlib.style.use(f'{prefix}sv.mplstyle')

def impulse(num_samples, a2, a1):
    '''calculates the impulse response of length num_samles for the two recursive factors a1, and a2'''
    x = numpy.zeros(num_samples)
    x[0] = 1.
    y = numpy.zeros(num_samples)
    for idx in range(num_samples):
        y[idx] = x[idx] - a1*y[idx-1] - a2*y[idx-2]
    return y
    
def onclick(event):
    '''on click the mark is set in the stability triangle and the resulting impulse response is calculated and displayed'''
    a1 = event.ydata
    a2 = event.xdata
    ax_stab.lines[0].set_data(a2, a1)
    y = impulse(num_samples, a2, a1)
    ax_impuls.cla()
    ax_impuls.stem(y, use_line_collection=True)
    ax_impuls.set(xlabel='Folgenkindex k ->', ylabel='Amplitude', title=f'Impulsantwort des Systems y[k] = x[k] - {a1:.3f}*y[k-1] - {a2:.3f}*y[k-2]', xlim=[0, num_samples-1], ylim=[-y.max(), y.max()])
    pyplot.draw()
    fig.canvas.draw_idle()

# creates triangle
edges = numpy.array([[-1, 0],[1, -2],[1, 2]])
triangle = pyplot.Polygon(edges[:], color='grey')

# coefficient values
a1 = 0.6
a2 = 0.9

# subplot figure
fig, (ax_stab, ax_impuls) = pyplot.subplots(1, 2)

# Stability Plot
ax_stab.add_patch(triangle)
ax_stab.set(xlabel=r'$a_2$', ylabel=r'$a_1$', title='Stabilitätsdreieck', xlim=[-2, 2], ylim=[-3, 3])
ax_stab.plot(a2, a1, 'X')

# Impulse Plot
num_samples = 50
y = impulse(num_samples, a1, a2)
ax_impuls.stem(y, use_line_collection=True)
ax_impuls.set(xlabel=r'Folgenkindex k $\rightarrow$', ylabel='Amplitude', title=f'Impulsantwort des Systems \n y[k] = x[k] - {a1:.3f}*y[k-1] - {a2:.3f}*y[k-2]', xlim=[0, num_samples-1])

# Execute onclick when button is pressed
cid = fig.canvas.mpl_connect('button_press_event', onclick)
pyplot.tight_layout()

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("Stabildreieck", fig, display=False)
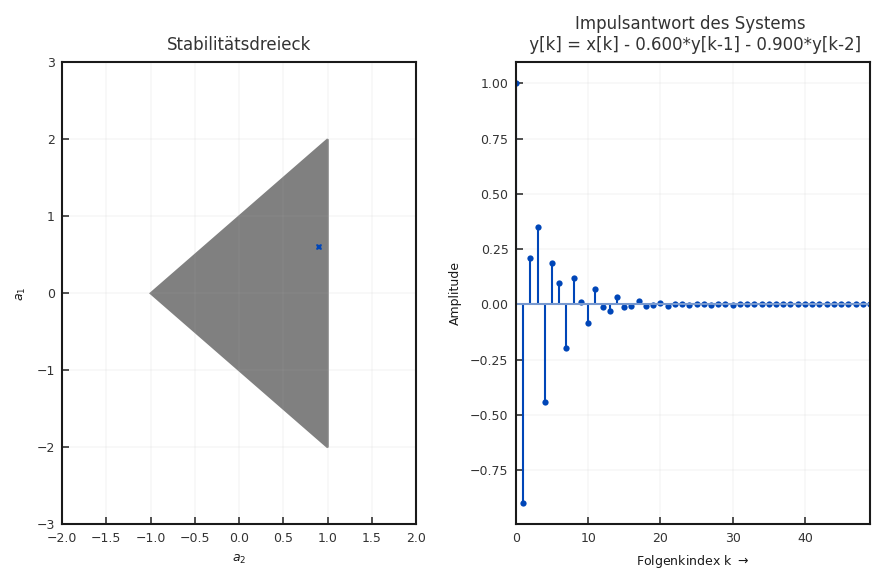
_images/ztrafo_20_1.png

Fig. 4.8 Stabilitätsdreieck für Systeme zweiter Ordnung mit den Koeffizienten \(a_1\) und \(a_2\).#

  1. Starten des interaktiven Programms - Signale_Stabilitätsdreieck.py in jupyterbook/code/interactive_programs/

  2. Per Linksklick Punkt im Dreieck auswählen

4.8. Interaktive Visualisierung der z-Transformation#

Für die Visualisierung der Interaktion von z-Transformation, dem im nächsten Kapitel vorgestellten Pol-Nullstellenplan und den dazugehörigen Übertragungsfunktionen steht auf

https://www.kvraudio.com/product/filterdemystifier-by-jadehochschule

ein Audio-Plugin (VST und AU) zur Verfügung, dass zusätzlich auch die Wirkung auf Audio-Signale zeigt. Der Source-Code ist ebenfalls öffentlich verfügbar (https://github.com/ArnoSchiller/FilterDeMystifier).

1

Würde gelten \(M>N\), könnte man durch Polynomdivision eine Übertragungsfunktion erhalten, die aus einem simplen Polynom und einer gebrochen rationalen Funktion mit \(M\leq N\) besteht, wobei das Polynom ein Polynom in \(z\) und nicht in \(z^{-1}\) wäre und somit bei einer z-Rücktransformation auf einen nicht-kausalen Anteil führen würde.