5. Spektren

Neben den zwei Beschreibungsebenen für diskrete Signale und Systeme, den Zeitbereich mit der Differenzengleichung und die z-Ebene, gilt ein besonderes Interesse, wie sich die Signale und Systeme in Abhängigkeit von der Frequenz verhalten. Diese Darstellung wird als Spektrum bezeichnet. Dabei ist das Betragsverhalten (Betragsspektrum), also ob und mit welcher Leistung eine Frequenz im Signal vorhanden ist oder ob ein System eine bestimmte Frequenz verstärkt oder dämpft, interessant. Das Phasenverhalten ist für viele Anwendungen von sekundärer Bedeutung. Trotzdem kann insbesondere bei der Beschreibung von Systemen das Phasenspektrum eine wichtige Information darstellen.

Beispiel

Motivationsbeispiel: Feedbackproblematik im Hörgerät oder bei der Bühnenbeschallung. Analyse des Signals (Spektrum) ermöglicht zu erkennen, bei welcher Frequenz die Störung auftritt. Nach der Analyse kann ein System eingebaut werden, dass die Übertragung bei dieser Frequenz dämpft. Durch den frequenzselektiven Eingriff wird das Nutzssignal nur unwesentlich beeinflusst.

ToDo

Das Motivationsbeispiel in einer konkreten Realisierung wäre schön.

Das Verhalten bei einer bestimmten Frequenz lässt sich z.B. testen, indem das LTI-System mit Signalen angeregt wird, die nur aus einer Frequenz bestehen und dann die Veränderung am Ausgang des Systems zu messen. Ein sehr gutes Eingangssignal um Betrag und Phase zu bestimmen ist die ungedämpfte diskrete Exponentialschwingung

(5.1)\[ e^{j\Omega_0 k} = \cos(\Omega k)+j\sin(\Omega k)~~~, \]

mit \(\Omega_0 = 2 \pi f_0/ f_\text{s}\), wobei \(f_0\) die Analysefrequenz und \(f_\text{s}\) die Samplingfrequenz angibt.

Exkurs: Frequenzachsen in der DSV

Manchmal ist es verwirrend in welcher Form Frequenzen in der digitalen Signalverarbeitung angegeben werden. Die am häufigsten verwendeten Systeme und ihre Äquivalenz als Achse und ihre Position auf dem Einheitskreis in der z-Ebene zeigt Abbildung 5.1 .

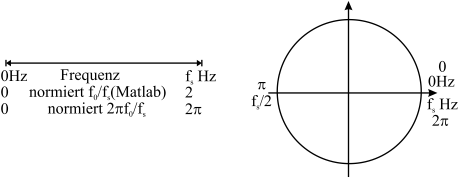
Fig. 5.1 Veranschaulichung der unterschiedlichen Frequenzbezeichnungen in der DSV und ihre Position auf dem Einheitskreis in der z-Ebene.

Mit Hilfe der Faltung ergibt sich am Ausgang eines durch die Impulsantwort beschriebenen Systems

(5.2)\[\begin{split}\begin{aligned} y(k)& = &x(k)\ast h(k) = \sum_{\kappa = -\infty}^{\infty} h(\kappa) e^{j\Omega_0(k-\kappa)}\\ &= & \underbrace{e^{j\Omega_0 k}}_{\mbox{Eingangssignal}} \cdot \underbrace{\sum_{\kappa = -\infty}^{\infty} h(\kappa) e^{-j\Omega_0 \kappa}}_{\mbox{Komplexer Multiplikator}}\end{aligned}~~~. \end{split}\]

Das heißt also, die am Ausgang gemessene Schwingung besitzt die gleiche Frequenz, die aber in ihrer Phase und ihrem Betrag geändert sein könnte. Die Berechnung dieses Ausgangsverhalten für alle Frequenzen führt zum gewünschten Spektrum. Auffällig bei LTI-Systemen ist, das keine neuen Frequenzen entstehen. Dies ist eine typische Eigenschaft von LTI-Systemen.

Wichtig

LTI-Systeme erzeugen keine neuen Frequenzen.

Bei Systemen wird die frequenzabhängige Veränderung des Betrages und der Phase Übertragungsfunktion genannt und durch

(5.3)\[ H(e^{j \Omega}) = \sum_{k = -\infty}^{\infty} h(k) e^{-j\Omega k} \]

berechnet. Dies entspricht einer Fourier-Transformation der nur zu diskreten Punkten definierten Impulsantwort. Allgemein kann jedes beliebige diskrete Signal so in den Frequenzbereich transformiert werden. Die dazugehörige Transformation wird Zeitdiskrete Fourier-Transformation (Discrete Time Fourier-Transformation, DTFT) genannt.

Vergleichen wir nun Gleichung (5.3) mit der Definition der z-Transformation, so ist zu erkennen, dass die DTFT die z-Transformation für \(z = e^{j\Omega}\) darstellt und somit genau den Einheitskreis in der z-Ebene beschreibt. Es kann also direkt am Einheitskreis das frequenzabhängige Übertragungsverhalten von Systemen abgelesen werden. Dies gilt analog natürlich auch für Signale.

Ist also die z-Transformation eines Systems bekannt kann auch sofort die Übertragungsfunktion angeben werden. Beispielsweise ergibt sich für das System \(y(k) = x(k) + x(k-1)\) mit \(e^{j\Omega}\) in die z-Transformierte eingesetzt

(5.4)\[ H(e^{j \Omega}) = 1+z^{-1} \Big|_{z = e^{j\Omega}} = 1+e^{-j\Omega}~~~. \]

Eine Multiplikation beider Seiten mit \(e^{j \Omega / 2}\) führt zu:

(5.5)\[\begin{split} \begin{aligned} e^{j\Omega / 2} H(e^{j \Omega}) &= & e^{j \Omega / 2}+e^{-j\Omega / 2}\\ H(e^{j \Omega}) & = & 2 \cos(\Omega / 2) e^{-j\Omega / 2} \end{aligned} \end{split}\]

Die komplexwertige Darstellung mit Real- und Imaginärteil ist dabei zur Veranschaulichung und Interpretation nicht geeignet. Statt dessen wird das komplexe Signal meist in den Betragsfrequenzgang, d.h, eine Darstellung von \(|H(e^{j \Omega})|\) über der Frequenz und den Phasengang, eine Darstellung des Arguments von \(H(e^{j \Omega})\), aufgeteilt, wobei bei dem Betrag oder dem Betragsquadrat auch häufig eine logarithmische Darstellung gewählt wird. In der Audiotechnik wird zusätzlich auch die Frequenzachse logarithmisch dargestellt, da dies eher der menschlichen Wahrnehmung von Tonhöhe entspricht.

5.1. Einfluss der Pole und Nullstellen auf die Übertragungsfunktion

Um den Einfluss der Pole und Nullstellen auf die Übertragungsfunktion abzuschätzen, hilft zunächst ein Besipiel. Abbildung 4.5 zeigt rechts \(|H(z)|^2\) als dreidimensionalen Höhenplot und \(|H(e^{j \Omega})|^2\) als schwarzen Einheitskreis in einer logarithmischen Darstellung. Der Betragsfrequenzgang der DTFT (schwarze Linie) kann direkt aus dem enstehenden “Gebirge” abgelesen werden, wenn der Einheitskreis vom Winkel \(0\) bis \(\pi\) umlaufen wird. Der Pol bei \(\pi/10\) verursacht eine Verstärkung auf dem Einheitskreis. Ein Pol direkt auf dem Einheitskreis würde zu einer unendlichen Verstärkung führen. Sobald der Winkel größer wird als \(\pi/10\) nimmt die Verstärkung ab. Ab einem Winkel von \(\pi/2\) werden die Nullstellen dominant, die dazu führen, dass sich der Betragsfrequenzgang null nähert und die Null bei genau \(\pi\) erreicht. Auf dem unteren Halbkreis geht zunächst der Einfluss der Nullstelle zurück und der konjugiert komplexe Pol bei \(-\pi/10\) gewinnt an Einfluss.\(\Omega = 2\pi\) entspricht erneut \(\Omega = 0\). Der Betragsfrequenzgang wiederholt sich also periodisch in \(2\pi\) für diskrete Signale. Dies ist auch direkt aus der Beziehung

(5.6)\[ e^{j\Omega k} = e^{j(\Omega +2\pi n) k} \quad \forall \quad n \in \mathbb{N} \]

zu sehen.

Eine direkte Berechnung des Betrag- und Phasenganges aus den Polen und Nullstellen ist ebenfalls möglich. Um das zu veranschaulichen ist in Abbildung 5.2 ein System zweiter Ordnung mit zwei Polen und zwei Nullstellen in der z-Ebene gezeigt.

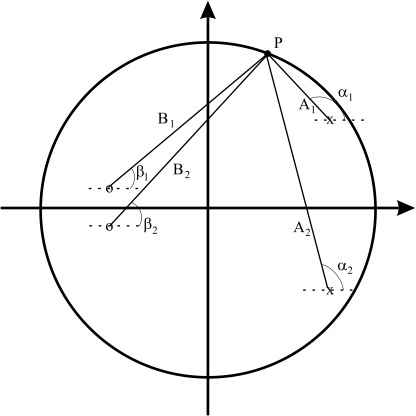
Fig. 5.2 Skizze zur Veranschaulichung des Einflusses von Polen und Nullstellen auf die Übertragungsfunktion \(H(e^{j \Omega})\).

Um den Betrag des Frequenzganges an der Stelle \(P\) zu berechnen, müssen die Abstände der Pole und Nullstellen zu diesem Punkt \(A_1, A_2,B_1,B_2\) bekannt sein. Er ergibt sich

(5.7)\[ \left|H(e^{j \Omega})\right|\Big|_{e^{j\Omega} = P} = |b_0| \frac{B_1 B_2}{A_1 A_2}. \]

Zusätzlich hat der Koeffizient \(b_0\) einen Einfluss, der aber aus dem Pol-Nullstellenplan nicht ersichtlich ist.

Die Phase an diesem Punkt kann durch

(5.8)\[ \arg\left\{H(e^{j \Omega}) \right\}\Big|_{e^{j\Omega} = P} = -\arg\{b_0\} + \beta_1 + \beta_2 - \alpha_1 - \alpha_2 \]

berechnet werden. Da \(b_0\) für reellwertige Systeme ebenfalls reell ist, kann der Term \(\arg\{b_0\}\) auch weggelassen werden, bzw. führt bei negativem \(b_0\) zu einer Phasendrehung von \(\pi\).

Für allgemeine Systeme mit einem Zählergrad \(M\) und einem Nennergrad \(N\) ergibt sich (angelehnt an [KK98])

(5.9)\[ \left|H(e^{j \Omega})\right| = |b_0| \frac{\displaystyle \prod_{i = 0}^{M-1} \sqrt{1-2|n_i|\cos(\Omega-\arg\{n_i\})+|n_i|^2}} {\displaystyle \prod_{i = 0}^{N-1}\sqrt{1-2|p_i|\cos(\Omega-\arg\{p_i\})+|p_i|^2}} \]

bzw. für die Phase

\(\renewcommand{\Re}[1]{\mathfrak{R}\left\{ #1 \right\}}\) \(\renewcommand{\Im}[1]{\mathfrak{I}\left\{ #1 \right\}}\)

(5.10)\[\begin{split} \begin{aligned} \arg\left\{H(e^{j \Omega})\right\} &=& (M-N)\Omega - \arg\{b_0\} \\\nonumber && + \sum_{i = 0}^{M-1}\arctan\left\{\frac{\sin \Omega-\Im{n_i}}{\cos \Omega- \Re{n_i}} \right\}\\\nonumber && - \sum_{i = 0}^{N-1}\arctan\left\{\frac{\sin \Omega-\Im{p_i}}{\cos \Omega-\Re{p_i}} \right\}\end{aligned} \end{split}\]

wobei \(\Re{\cdot}\) und \(\Im{\cdot}\) den Real- bzw. Imaginäranteil einer komplexen Zahl symbolisieren.

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

#%matplotlib inline
import time
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as signal
import ipywidgets as widgets
from IPython.display import display

radius_poles = 0.9
omega_poles = np.pi / 10

pole_list = [radius_poles * np.exp(1j*omega_poles)]
pole_list.append(pole_list[0].conjugate())


radius_zeros = 0.95
omega_zeros = 7 * np.pi / 10

zero_list = [radius_zeros * np.exp(1j*omega_zeros)]
zero_list.append(zero_list[0].conjugate())


# from poles and zeros, compute system coefficients
a_coefficients = np.poly(pole_list)
b_coefficients = np.poly(zero_list)

# draw poles and zeros
#plt.figure(1)
#plt.scatter(np.real(pole_list), np.imag(pole_list), marker='x', c='r')
#plt.scatter(np.real(zero_list), np.imag(zero_list), marker='o', c='b')

# draw unit circle inside the same plot
angles_rad = np.linspace(0, 2*np.pi, 512)
#plt.plot(np.cos(angles_rad), np.sin(angles_rad), c='k')

# plot formatting stuff
#plt.axis('equal')
#plt.grid()
#plt.title('Pol-Nullstellen-Plan')
#plt.xlabel('Re(z)')
#plt.ylabel('Im(z)')
#plt.show()
# compute complex-valued transfer function
_, transfer_function = signal.freqz(b_coefficients, a_coefficients, whole=True)


# def pole_zero_influence_plot(spec_idx):
    
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(15, 5))

# first subplot: pole-zero plot
ax[0].scatter(np.real(pole_list), np.imag(pole_list), marker='x', c='r')
ax[0].scatter(np.real(zero_list), np.imag(zero_list), marker='o', c='b')
ax[0].plot(np.cos(angles_rad), np.sin(angles_rad), c='k')
ax[0].set(aspect='equal')

# second subplot: magnitude of transfer function
ax[1].plot(20*np.log10(np.abs(transfer_function)))
ax[1].set_xlim([0, len(transfer_function)])
ax[1].set_ylim([-40, 40])

# second subplot: phase of transfer function
ax[2].plot(np.angle(transfer_function))
ax[2].set_xlim([0, len(transfer_function)])

ax[2].set_ylim([-np.pi, np.pi])

# draw lines from each pole to the current index
#or pole_idx in range(0, len(pole_list)):
#   ax[0].plot([np.cos(angles_rad[spec_idx]), np.real(pole_list[pole_idx])],
#              [np.sin(angles_rad[spec_idx]), np.imag(pole_list[pole_idx])], ':')

# draw lines from each zero to the current index
#or zero_idx in range(0, len(zero_list)):
#   ax[0].plot([np.cos(angles_rad[spec_idx]), np.real(zero_list[zero_idx])],
#              [np.sin(angles_rad[spec_idx]), np.imag(zero_list[zero_idx])], ':')

# plot markers into transfer function plots at the same index
#x[1].plot([spec_idx, spec_idx], [-40, 20*np.log10(np.abs(transfer_function[spec_idx]))])
#x[2].plot([spec_idx, spec_idx], [-np.pi, np.angle(transfer_function[spec_idx])])

        

# create a slider that uses the slider value inside of the plot function
# interactive_plot = widgets.interactive(pole_zero_influence_plot, spec_idx=(1, len(transfer_function)-1, 5))

# show the slider and the plot
# interactive_plot

(-3.141592653589793, 3.141592653589793)

To Do

Phase muss noch deutlich besser erklärt werden und die folgenden Interpretationen sollten durch Besipiele (plots mit Python) gezeigt werden. Plot fuer ein PN Plan siehe oben

Eine Interpretation (die Nutzung vom FilterDeMystifier hilft hier sehr, siehe Abschnitt 4.8) führt zu den Schlüssen:

• Je näher ein Pol am Einheitkreis liegt umso größer ist sein Einfluss auf die Übertragungsfunktion.

• Eine Nullstelle auf dem Einheitskreis führt zu einem Phasensprung um \(\pi\).

• Systeme, bei denen alle Nullstellen im inneren des Einheitskreises liegen, heißen minimalphasig.

• Pole oder Nullstellen im Ursprung verändern nur die Phase, aber nicht den Betrag der Übertragungsfunktion.

• Nullstellen die am Einheitskreis gespiegelt werden (\(r_\text{out} = 1/r_\text{in}\)), führen nur zu einer Veränderung der Grundverstärkung des Betrages der Übertragungsfunktion aber nicht zu einer Veränderung der Form. Gleichzeitig wird aber die Phase so verändert, dass sie um über \(180^{\circ}\) dreht und das resultierende System nicht mehr minimalphasig ist.

• Systeme bei denen die Nullstellen an den Positionen der am Einheitskreis gespiegelten Pole liegen

  (5.11)\[ n_{i_0} = \frac{1}{p_{i_{\infty}}} \]

  heißen Allpasssysteme, da der Betrag für alle Frequenzen konstant bleibt. Nur die Phase wird verändert und dreht um \(N \pi\), wobei \(N\) die Ordnung des Systems angibt.

5.2. Diskrete Fourier-Transformation

Zur Frequenzanalyse ist bisher nur die DTFT bekannt. Aber diese Transformation kann nicht auf einem Computer umgesetzt werden, da das resultierende Spektrum nicht diskret ist. Außerdem benötigt man unendlich viele Eingangswerte um das Spektrum zu berechnen. Deshalb wird in einem ersten Schritt die Anzahl der genutzten Abtastwerte auf \(N\) beschränkt. Man könnte dies auch so interpretieren, dass die unendliche Folge des Signals mit einer Rechteckfolge der Höhe eins und der Länge N multipliziert wird. Da außerhalb des Eins-Bereichs alle Multiplikationen zu Null werden, können auch die Summengrenzen verändert werden.

Diese Rechteckfolge werden wir im weiteren mit Fenster oder Window bezeichnen, da es aus der Folge nur einen Ausschnitt zeigt, in Anlehnung an ein Glasfenster, das uns nur einen Ausschnitt der Wirklichkeit zeigt (siehe Abbildung 5.3s). Die Länge \(N\) nennen wir Blockgröße, da nur noch ein Block mit Daten verarbeitet wird.

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

import matplotlib
import numpy
import matplotlib.pyplot as pyplot

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

matplotlib.style.use(f'{prefix}sv.mplstyle')

fig, ax = pyplot.subplots(nrows=3, ncols=1)
ax_signal = ax[0]
signal = numpy.random.random_sample(36)*4 - 2 # random sample scaled -2 to 2
ax_signal.stem(range(-10,26), signal, use_line_collection=True)
ax_signal.set(xlabel='Folgenkindex k ->', ylabel='Amplitude x[k]', 
        title='Eingangssignal', xlim=[-10, 26])

ax_window = ax[1]
window = numpy.concatenate([[0]*10, [1]*16, [0]*10])
ax_window.step(range(-10,26), window, where='mid')
ax_window.set(xlabel='Folgenkindex k ->', ylabel='Amplitude x[k]', 
        title='Rechteck-Fensterfunktion', xlim=[-10, 26])

ax_filtered = ax[2]
filtered_signal = signal * window # filtering in time domain
ax_filtered.stem(range(-10,26), filtered_signal, use_line_collection=True)
ax_filtered.set(xlabel='Folgenkindex k ->', ylabel='Amplitude x[k]', 
        title='gefenstertes Signal', xlim=[-10, 26])

pyplot.tight_layout()

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("DFT_FensterMultiplikation", fig, display=False)

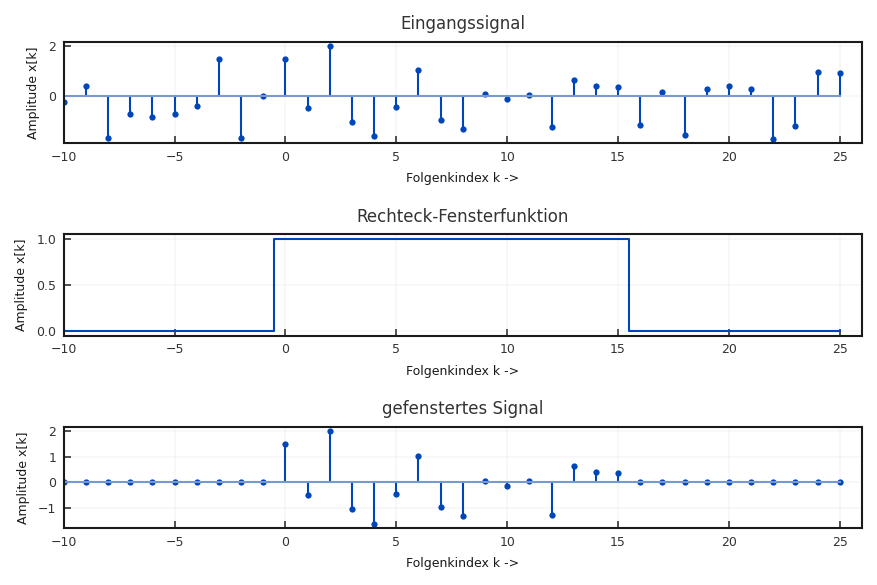
Fig. 5.3 Veranschaulichung der Wirkung einer Rechteck-Fensterfunktion der Länge \(N = 16\).

Das resultierende Spektrum ist aber immer noch kontinuierlich. Durch die periodische Wiederholung des Spektrums ist es aber ausreichend nur den Bereich von \(0 \leq \omega\leq 2\pi\) genauer zu betrachten. Um eine diskretes Spektrum zu erhalten, unterteilen wir das Spektrum in \(N\) gleichförmige Abschnitte (es kann eine beliebige Anzahl verwendet werden, eine Zweierpotenz führt aber zu besonders effizienten Lösungen).

Die DTFT geht damit in

(5.12)\[ X(n) = X\left(e^{j 2 \pi n / N}\right) = \sum_{k = 0}^{N-1}x(k) e^{-j 2 \pi n k /N} \]

über.

Umgekehrt ist es natürlich auch möglich, aus den \(N\) Spektralwerten auf die Folge \(x(k)\) zurückzuschließen. Die Rücktransformation

(5.13)\[ x(k) = \frac{1}{N} \sum_{n = 0}^{N-1}X(n) e^{j 2 \pi n k /N} \]

enthält zusätzlich noch einen Normierungsterm \(N\) und unterscheidet sich sonst nur in dem Vorzeichen der e-Funktion.

Das Transformationspärchen (5.12) und (5.13) werden als diskrete Fourier-Transformation (DFT), bzw. inverse DFT (IDFT) bezeichnet.

5.3. Eigenschaften

5.3.1. Zusammenhang DTFT und DFT

Wir haben, um von der exakten Darstellung des Spektrums mittels DTFT auf die computerlösbare DFT zu kommen, zwei Veränderungen vorgenommen. Und natürlich spiegeln sich diese Veränderungen auch im Ergebnis wieder. Wir müssen also versuchen, die Veränderungen zu analysieren, um sicher zu sein, dass die DFT zumindest eine Näherung der DTFT ist.

Zunächst ist es interessant die vorgenommene Diskretisierung im Frequezbereich zu untersuchen. Im Grunde genommen haben wir das Spektrum abgetastet. Die Konsequenz der Abtastung kennen wir bereits aus der normalen Abtastung im Zeitbereich. Es kommt zu einer periodischen Wiederholung des Spektrums. Die Abtastung im Frequenzbereich führt zu einer periodischen Wiederholung im Zeitbereich. Wenn man also ein Signal analysiert und zurück transformiert ergibt sich eine periodische Wiederholung. Auch hier gibt es eine andere Interpretationsmöglichkeit. Bei der Analyse von periodischen Signalen mittels Fourier-Reihen ergeben sich diskrete Spektren. Ein diskretes Spektrum führt im Umkehrschluss also zu einer periodischen Zeitfunktion, wobei bei der DFT die Periode genau \(N\) ist (siehe Abbildung 5.4).

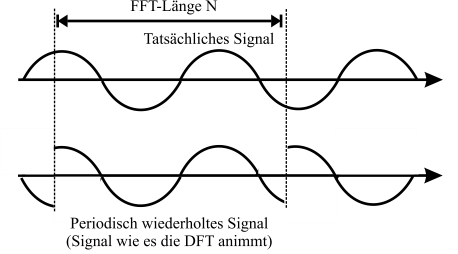
Fig. 5.4 Veranschaulichung der erzwungenen Signalperiodizität durch die DFT.

Der Einfluss der Fenster-Funktion lässt sich zunächst nur durch die DTFT beschreiben. Es ist bekannt, dass eine Faltung im Zeitbereich zu einer Multiplikation im Bildbereich (Frequenzbereich) führt. Das Umgekehrte gilt aber auch. Eine Multiplikation im Zeitbereich, und damit die Nutzung des Fensters, ist eine Multiplikation. Sie führt im Frequenzbereich zu einer Faltung der Spektren, wobei die Faltung hier kontinuierlich als Integral zu definieren ist, da wir ja ein kontinuierliches periodisches Spektrum haben.

(5.14)\[ H(e^{j \Omega}) \Big|_{0 \leq n \leq N} = \int_{\theta = -\pi}^{\pi} H (e^{j\theta}) H^{W}(e^{j(\Omega - \theta)})\text{d}\theta \]

wobei \(H^{W}\) die Übertragungsfunktion der Fensterfunktion ist.

Für das Rechteckfenster ergibt sich das Spektrum, indem wir zunächst die z-Transformation der Fensterfolge \(w(k)\) ansetzen. Es gilt

\[ H^{W}(z) = \sum_{k = -\infty}^{\infty} w(k) z^{-k} = \sum_{k = 0}^{N-1} z^{-k}~~~. \]

Durch einsetzen von \(z = e^{j\Omega}\) ergibt sich das Spektrum

\[ H^{W}(z)\Big|_{z = e^{j\Omega}} = \sum_{k = 0}^{N-1} e^{-j\Omega k}~~. \]

Mit der Formel der endlichen geometrischen Reihe2 erhält man das Spektrum der Rechteckfunktion

\[\begin{split} \begin{aligned} H^{W}(e^{j \Omega}) & = & \frac{1-e^{-j\Omega N}}{1- e^{-j\Omega}}\\ & = & \frac{e^{-j\Omega N/2} \overbrace{(e^{j\Omega N/2}- e^{-j\Omega N/2})}^{2j\sin(\Omega N/2)}} {e^{-j \Omega/2}\underbrace{(e^{j \Omega/2}- e^{-j\Omega/2})}_{2j\sin(\Omega/2)}}\\ & = & e^{-j(N-1)\Omega/2}\frac{\sin\left(N \Omega/2 \right)}{\sin\left(\Omega/2 \right)}\end{aligned} \end{split}\]

Der vordere Teil dieser Funktion entspricht einer linearen Phasenverschiebung. Der zweite Teil mit den Sinustermen stellt eine sogenannte Dirichlet-Funktion dar. Der Betrag dieser Funktion ist in Abbildung 5.5 gezeigt.

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

import matplotlib
import numpy
from matplotlib import pyplot

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

matplotlib.style.use(f'{prefix}sv.mplstyle')

N = 16 # filter length
freqs = numpy.linspace(-3, 3, 600) # frequency vector
dirichlet = [0]*len(freqs) 
for idx in range(len(freqs)):
    # calculate dirichlet function with sin(N*w/4)/sin(w/4)
    dirichlet[idx] = numpy.sin(N*freqs[idx]*numpy.pi*0.5)/ \
            numpy.sin(freqs[idx]*numpy.pi*0.5)

# normalizing
dirichlet_abs = numpy.abs(dirichlet)/numpy.abs(dirichlet).max()

fig, ax_dirichlet = pyplot.subplots()
ax_dirichlet.plot(freqs, dirichlet_abs)
ax_dirichlet.set(xlabel='Frequenz rad/pi ', 
        ylabel='Frequenzanteil normiert auf 1', 
        title='Spektrum eines Rechteckfenster (Dirichlet-Funktion)')

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("DirichletFkt", fig, display=False)

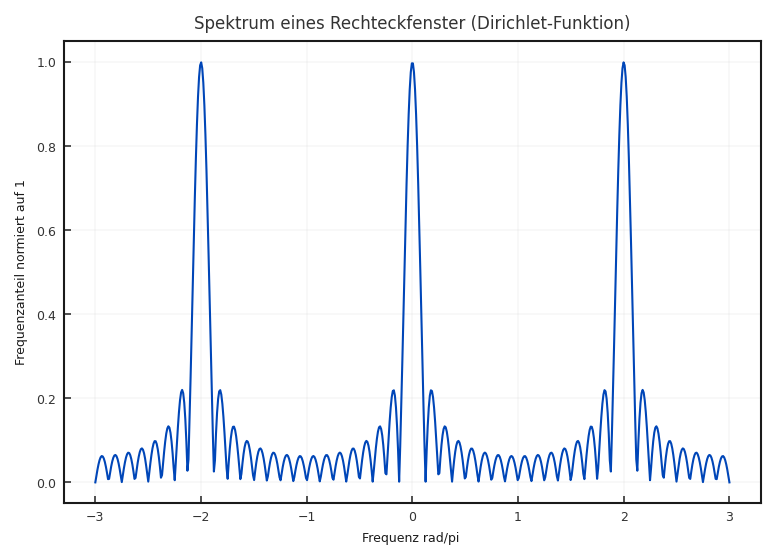
Fig. 5.5 Betrag von \(H^{W}(e^{j \Omega})\) für \(N = 16\).

Beispiel: DTFT und DFT bei einer Cosinus-Schwingung

Um die Unterscheide zwischen DTFT und DFT bei der Spektrumsberechnung eines Cosinus aufzuzeigen, müssen wir zunächst das Spektrum einer abgetasteten Cosinusschwingung berechnen:

\[\begin{split} \begin{aligned} H(e^{j \Omega}) & = & \sum_{-\infty}^{\infty} \cos \left(k \Omega_0 \right) e^{-j\Omega k}\\ & = & \sum_{-\infty}^{\infty} \frac{1}{2}\left( e^{j k \Omega_0} + e^{-j k \Omega_0}\right) e^{-j\Omega k}\\ & = & \sum_{-\infty}^{\infty} \frac{1}{2} \left( e^{j k (\Omega_0-\Omega)} + e^{-j k (\Omega_0 + \Omega)}\right)\\ & = & \sum_{-\infty}^{\infty} \frac{1}{2} e^{-j k (\Omega-\Omega_0)} + \sum_{-\infty}^{\infty} \frac{1}{2} e^{-j k (\Omega + \Omega_0)}\\ & = & \frac{1}{2} \delta^D(\Omega - \Omega_0) + \frac{1}{2} \delta^D(\Omega + \Omega_0)~~~, \end{aligned} \end{split}\]

mit \(\Omega = 2\pi f / f_\text{s}\). Das heißt, das Spektrum des abgetasteten Cosinus hat nur zwei definierte Frequenzwerte, an den Frequenzen \(\Omega = \pm \Omega_0\).

Um den Einfluss der Annäherung durch die DFT zu veranschaulichen, begrenzen wir den betrachteten Signalausschnitt auf \(N\) Datenwerte. Dies führt wie in Gleichung (5.14) gezeigt zu einer Faltung mit dem Spektrum des Rechtecks. Durch die Siebeigenschaft der \(\delta\)-Funktion ergibt sich

\[\begin{split} \begin{aligned} H(e^{j \Omega}) & = & \left(\frac{1}{2} \delta \left(\Omega - \Omega_0 \right) + \frac{1}{2} \delta \left(\Omega + \Omega_0 \right) \right) \ast H^{W}(e^(j \Omega)) \\ & = & \frac{1}{2} H^{W} \left(e^{j(\Omega -\Omega_0 )}\right) + \frac{1}{2} H^{W} \left(e^{j(\Omega + \Omega_0 )}\right).\end{aligned} \end{split}\]

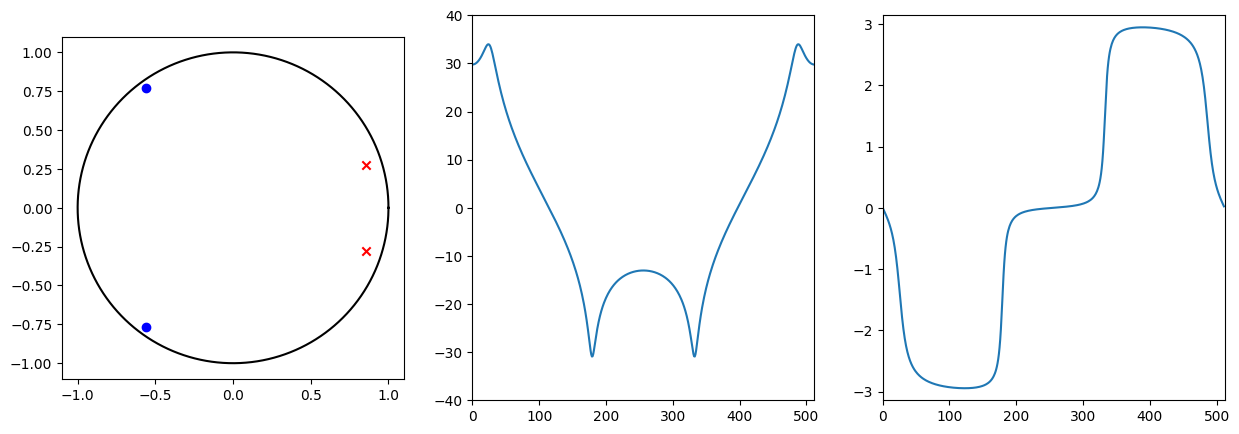
Das Spektrum des Rechtecks wird also, um \(\pm \Omega_0\) verschoben. Abbildung 5.6 zeigt das resultierende Spektrum für \(N =\) 16 bei einer Grundfrequenz von \(f_0 =\) 155 Hz und einer Abtastrate von \(f_\text{s} =\) 1 kHz.

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

import matplotlib
import numpy
from matplotlib import pyplot

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

matplotlib.style.use(f'{prefix}sv.mplstyle')

num_samples = 16
f0 = 155
fs = 1000

sample = [0]*num_samples

kk = numpy.arange(num_samples)
cos_series = numpy.cos(2*numpy.pi*f0*kk/fs)

sample = numpy.concatenate(([0]*4,cos_series,[0]*4))

reconst_sig = numpy.concatenate((cos_series[-4:],cos_series,cos_series[0:4]))


# signal reconstruction from fft through ifft
spectrum = numpy.fft.fft(sample,256)
spectrumshort = numpy.fft.fft(sample)

spectrumshort = numpy.fft.fftshift(numpy.abs(spectrumshort)/numpy.abs(spectrumshort).max())
spectrum = numpy.fft.fftshift(spectrum)
# dB normalized to 0 max amplitude
spectrum_abs = numpy.abs(spectrum)/numpy.abs(spectrum).max() 
# frequency bins for plotting
freqs_fft = numpy.linspace(-1, 1, len(spectrum_abs)) 
freqs_fftshort = numpy.linspace(-1, 1, len(spectrumshort)) 


fig, ax = pyplot.subplots(2, 2)
ax[0][0].stem(range(-4,len(sample)-4),sample)
ax[0][0].set(xlabel='Folgenndex k ->', ylabel='Amplitude x[k]', 
        title='Eingangssignal Sinus')

ax[0][1].plot(freqs_fft, spectrum_abs)
ax[0][1].set(xlabel='Frequenz rad/pi ', 
        ylabel='Frequenzanteil normiert auf 1', 
        title='Amplitudenspektrum der gefensterten Cosinus-Fkt')

ax[1][0].stem(freqs_fftshort, spectrumshort, use_line_collection=True)
ax[1][0].set(xlabel='Frequenz rad/pi ', 
        ylabel='Frequenzanteil normiert auf 1',
        title='Abgetastetes Amplitudenspektrum')

ax[1][1].stem(range(-4,len(sample)-4),reconst_sig)
ax[1][1].set(xlabel='Folgenndex k ->', ylabel='Amplitude x[k]', 
        title='durch Abtastung des Spektrums erzieltes rekonstruiertes Signal')
ax[1][1].plot([-0.5,-0.5],[-1,1], 'r:' )
ax[1][1].plot([15.5,15.5],[-1,1], 'r:')

pyplot.tight_layout()

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("DFT_Cosinus", fig, display=False)

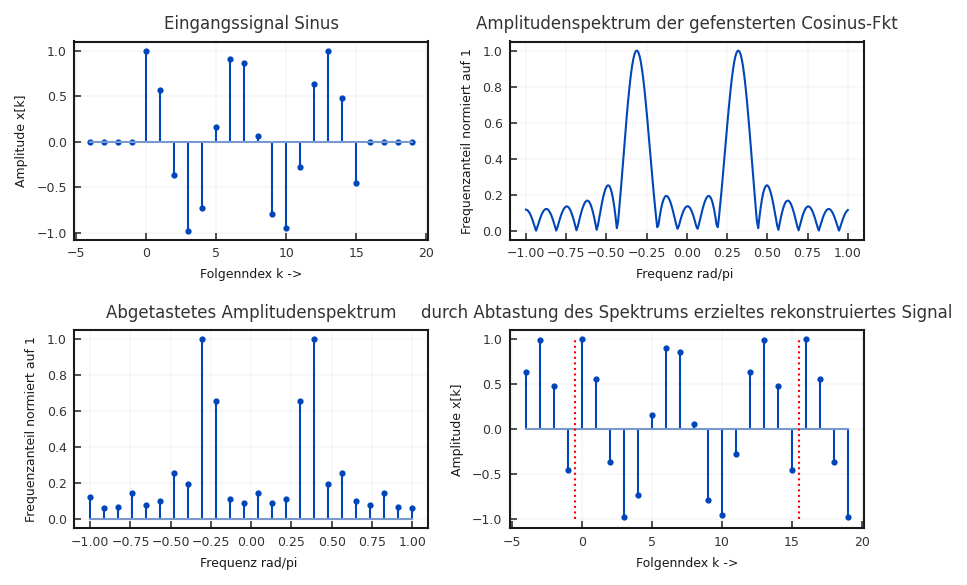
Fig. 5.6 Spektrum (rechts) eines abgetasteten Cosinus (links), der auf \(N = \)16 Werte begrenzt wird (\(f_s = \)1 kHz und \(f_0 = \)155 Hz).

Um nun das DFT-Spektrum zu berechnen ist zusätzlich die Abtastung im Frequenzbereich notwendig. Dies hat implizit zur Folge, dass die Cosinusfolge periodisch wiederholt wird. Das abgetastete Spektrum ist auf der unteren linken Seite in Abbildung Abbildung 5.6 zu sehen und die resultierende Folge auf der rechten Seite.

Das resultierende Spektrum hat nicht das erwartete Maximum bei \(f_0\), da 155 Hz nicht im Abtastraster einer 16 Punkte FFT bei einer Abtastrate von 1 kHz liegt. Statt dessen ist die Leistung des Cosinus über viele Abtastpunkte spektral verteilt. Dieser Effekt wird auch als Leakage bezeichnet.

To Do

Beispiele mit anderen Frequenzen, um zu zeigen, dass Dirichlet- Funktion abgetastet wird.

5.3.2. Symmetrien der DFT

Eine der wichtigsten Symmetrien für die diskrete sowie für die zeitdiskrete Fourier-Transformation (DFT und DTFT) ergibt sich für reelle Signale. Aus den Eigenschaften der z-Transformation ist deutlich, dass sich nur dann reelle Koeffizienten bei Signalen und Systemen ergeben, wenn die Pole und Nullstellen konjugiert komplex auftreten. Daraus folgt, dass die Spektren reeller Signale konjugiert komplex sind. Es ergibt sich also eine Symmetrie der Spektren an der Null-Hertz-Linie (Gleichstrom). Der Realteil ist dabei achsensymmetrisch (gerade) und der Imaginärteil punktsymmetrisch (ungerade). Diese Symmetrien ergeben sich auch, wenn Betrag und Phase betrachtet werden. Der Betrag reeller Funktionen ist immer achsensymmetrisch und die Phase punktsymmetrisch (siehe Abbildung 5.7).

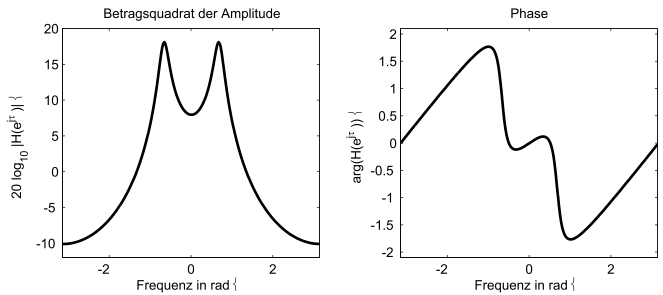
Fig. 5.7 Beispiel eines Frequenz- und Phasenverlaufs eines reellwertigen Systems.

Die Symmetrien lassen sich bei der Berechnung der DFT und IDFT ausnutzen, da immer nur das halbe Spektrum berechnet werden muss, während die andere Hälfte durch Spiegelung erzeugt werden kann. Häufig kommt es vor, dass man im Spektralbereich etwas berechnet und an der dazugehörigen Zeitfolge interessiert ist (zum Beispiel bei einen Filterentwurf). Es reicht aus, für eine \(N\)-Punkte DFT, \(N/2+1\) Spektralwerte zu kennen. Man benötigt einen Wert mehr, da die DFT für die höchste Frequenz bei \(f_\text{s}/2\) nur einen reellwertigen Koeffizienten besitzt. Die Kopiervorschrift in Matlab sieht dann wie folgt aus, wobei wir annehmen, dass die \(N/2+1\) Werte in H_halb gespeichert sind.

Matlab

    H_voll = [H_halb conj(H_halb(end-1:-1:2))];

Python

    H_halb_c = H_halb[:,-1}]
    H_voll = H_halb + H_halb_c

Entsteht nach der Rücktransformation eine rein reellwertige Folge, wurden alle Symmetrien richtig aufgebaut. Dies kann als Gegenprobe verwendet werden, wobei die resultierende Variable durch Rundungsfehler bei der elektronischen Verarbeitung immer komplex ist. Es ist deshalb notwendig, den Betrag des Imaginäranteils zu überprüfen. Dieser sollte Werte um \(10^{-7}\) nicht überschreiten.

Wie lässt sich die Symmetriebedingung mathematisch zeigen?

Ausgehend von

\[ X(n) = \sum_{k = 0}^{N-1} x(k) e^{-jkn2\pi/N} \]

ergibt sich für die an der y-Achse gespiegelte Folge durch Variablensubstitution

\[ X(-n) = \sum_{k = 0}^{N-1} x(k) e^{jkn2\pi/N}~~~. \]

Konjugiert man dieses Signal ergibt sich

\[ X^{\ast}(-n) = \sum_{k = 0}^{N-1} e^{-jkn2\pi/N}~~~, \]

wobei der negative Exponent zu beachten ist. Für ein reelwertiges Signal gilt \(x^{\ast}(k) = x(k)\), woraus folgt, dass

\[ X^{\ast}(-n) = X(n)~~~. \]

5.3.2.1. Spektren reeller gerader Folgen

Die Symmetriebedingung reeller gerader Folgen kann aus den vorherigen Überlegungen geschlossen werden. Da gerade Funktionen achsensymmetrisch sind, der Imaginärteil aber punktsymmetrisch, können wir schließen, dass reelle, gerade Funktionen ein reelles, gerades Spektrum haben.

5.3.3. Rechenregeln

5.3.3.1. Linearität

Die DFT ist eine lineare Transformation. Es gilt also das Superpositionsprinzip

(5.15)\[ a_1 x_1(k) + a_2 x_2(k) ;\circ \hskip-1ex -\hskip-1.2ex -\hskip-1.2ex- \hskip-1ex \bullet\; a_1 X_1(n) + a_2 X_2(n)~~~. \]

5.3.3.2. Faltung

Bisher haben wir bereits die Faltung bei der z-Transformation kennen gelernt und den Übergang der Faltung in die Multiplikation in der z-Ebene. Dieser Zusammenhang gilt auch für die DTFT, aber nicht so direkt für die DFT. Um das zu veranschaulichen, kann ein einfaches Beispiel dienen. Gehen wir davon aus, dass wir eine Folge mit \(N = 8\) Werten mit Hilfe der DFT in den Bildbereich transformieren. Wir erhalten 8 Frequenzpunkte. Des Weiteren transformieren wir eine zweite Folge mit 8 Datenwerten. Wir erhalten erneut 8 Spektralwerte. Multiplizieren wir diese beiden Spektren und führen eine Rücktransformation durch, so besteht das Ergebnis auch aus 8 Werten im Zeitbereich. Aus der Faltungsalgebra wissen wir aber, dass das Faltungsprodukt aus \(L+M-1\) Elementen bestehen muss, in diesem Beispiel also 15 Datenwerte. Daraus folgt, dass die Faltung nicht der Multiplikation mit den DFT-Spektralwerten entspricht.

Die Ursache hierfür ist in der implizierten Periodizität der DFT zu finden. Das DFT Spektrum ist gerade nicht das Signal im betrachteten Zeitfenster, sondern ein Signal das periodisch fortgesetzt ist. Die Multiplikation im Frequenzbereich führt deshalb auf eine Faltung dieser periodisch fortgesetzten Sequenzen. Dies führt dazu, dass auch das Faltungsprodukt periodisch ist. Man spricht deshalb von der zyklischen Faltung. Das Ergebnis kann sich vollständig von dem gewünschten Ergebnis unterscheiden. Dies wird in Abbildung 5.8 demonstriert. Die beiden Folgen (a, b) ergeben bei der Faltung im Zeitbereich die Folge c. Die Lösung mit Hilfe der DFT führt auf die Folge d.

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

import matplotlib
import numpy
from matplotlib import pyplot

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

matplotlib.style.use(f'{prefix}sv.mplstyle')

# input samples
a = [1, 2, 3, 4, 5, 6, 7, 8]
b = [1, 2, 3, 4, -1, -2, -3, -4]

# usual convolution
usual_convolution = numpy.convolve(a, b)

# cyclical convolution, equal to multiplying spectra
dft_spektrum = numpy.fft.fft(a) * numpy.fft.fft(b)
zyklische_faltung = numpy.fft.ifft(dft_spektrum)


fig, ((ax_a, ax_b), (ax_ab, ax_fft)) = pyplot.subplots(2, 2)

ax_a.stem(a, use_line_collection=True)
ax_a.set(xlabel='Folgenndex k ->', ylabel='Amplitude x[k]', title='Signal A')
ax_b.stem(b, use_line_collection=True)
ax_b.set(xlabel='Folgenndex k ->', ylabel='Amplitude x[k]', title='Signal B')
ax_ab.stem(usual_convolution, use_line_collection=True)
ax_ab.set(xlabel='Folgenndex k ->', ylabel='Amplitude', 
        title='Konventionelle Faltung')
ax_fft.stem(zyklische_faltung, use_line_collection=True)
ax_fft.set(xlabel='Folgenndex k ->', ylabel='Amplitude', 
        title='Zyklische Faltung')

pyplot.tight_layout()

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("BspZyklischeFaltung", fig, display=False)

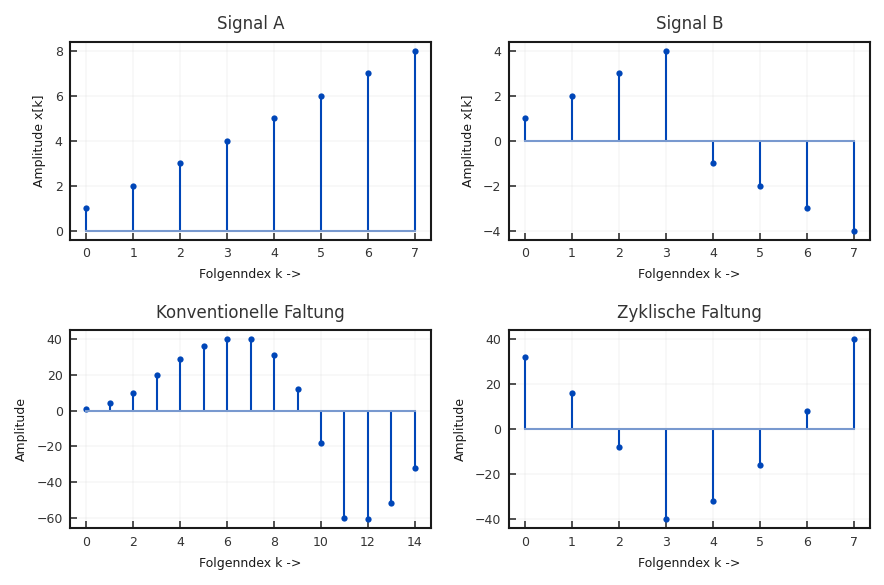
Fig. 5.8 Beispiel für zyklische Faltung. Die beiden Folgen (Bild a,b) ergeben bei konventioneller Faltung Bild c. Bild d zeigt das Resultat für die direkte Faltung im Frequenzbereich mit Hilfe der DFT.

Um die zyklischen Faltungsprodukte zu verhindern ist es notwendig Nullen an die zu transformierenden Folgen anzuhängen (Zero-Padding) und eine entsprechend größere Transformationslänge zu wählen. Dies führt dazu, dass die implizite Periodizität die Nullen einschließt. Die Nullen verändern das Spektrum nicht, sondern nur die Frequenzauflösung3. Die Rücktransformation führt zu der gewünschten Faltungsfolge, wobei durch die vorher eingebrachten Nullen keine zyklischen Faltungsprodukte das Ergebnis verfälschen. Bei dem obigen Beispiel würde sich das Ergebnis in Abbildung 5.8 c ergeben, wenn an die Folgen a und b jeweils 8 Nullen angehängt werden und die DFT Länge auf 16 erhöht wird.

To Do

Einfacheres Beispiel mit Rechteck und Dreiecksfunktionen, bei denen die Wiederholungen eingezeichnet sind.

5.3.3.3. Theorem von Parseval

Das Theorem von Parseval sagt aus, dass man die Energie eines Signals im Zeit, oder im Frequenzbereich berechnen kann, bzw. dass die Leistung eines Signals im Zeit- und Frequenzbereich gleich ist. Für die DTFT gilt

(5.16)\[ \sum_{k = -\infty}^{\infty} x^2(k) = \frac{1}{2\pi} \int_{-\pi}^{\pi} \left|X(e^(j \Omega)) \right|^2 \text{d}\Omega~~~, \]

bzw. für die DFT

(5.17)\[ \sum_{k = 0}^{N-1} x^2(k) = \frac{1}{N}\sum_{n = 0}^{N-1} |X(n)|^2~~~. \]

5.3.4. Effiziente Implementierung

Die DFT lässt sich durch Ausnutzung unterschiedlicher Symmetrien sehr effizient berechnen. Um dies zu verdeutlichen, soll das sogenannten Decimation in Time-Verfahren zur drastischen Reduktion der benötigten Rechenleistung genauer gezeigt werden. Andere Verfahren können in der sehr umfangreichen Literatur zur Entwicklung der Fast Fourier Transform (FFT) gefunden werden [Coo90, KK98, OS99].

Um eine effiziente Realisierung zu finden, legen wir die Länge der FFT als Zweierpotenz fest. Besonders häufig in der Audio und Sprachsignalverarbeitung genutzte FFT-Längen sind 256, 512, 1024 und 2048. Durch diese Forderung ist es möglich, die Folge in zwei Teilfolgen zu zerlegen, wobei wir immer abwechselnd die Elemente der Folge den jeweiligen neuen Teilfolgen zuordnen. Es ergeben sich die Folgen \(x(2k)\) und \(x(2k+1)\) (siehe Abbildung 5.9).

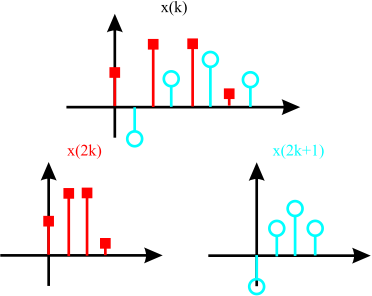
Fig. 5.9 Aufteilung einer Sequenz in zwei Teilsequenzen zur Erklärung der FFT (Decimation in Time)

Die Konsequenzen für die DFT lassen sich nun wie folgt berechnen:

\[\begin{split} \begin{aligned} \nonumber \sum_{k = 0}^{N-1} x(k) e^{-j 2 \pi n k /N} & = & \sum_{k = 0}^{\frac{N}{2}-1} \underbrace{x(2k)}_{u(k)} e^{-j 2 \pi n 2k /N} + \sum_{k = 0}^{\frac{N}{2}-1} \underbrace{x(2k+1)}_{v(k)} e^{-j 2 \pi n (2k+1) /N} \\\nonumber & = & \underbrace{\sum_{k = 0}^{\frac{N}{2}-1}u(k) e^{-j 2 \pi n k /\frac{N}{2}}}_{U(n) \qquad \mbox {N/2 DFT}} + e^{-j2\pi n /N} \underbrace{\sum_{k = 0}^{\frac{N}{2}-1} v(k) e^{-j 2 \pi n k /\frac{N}{2}}}_{V(n) \qquad \mbox {N/2 DFT}}\\ X(n) & = & U(n) + e^{-j2\pi n /N} V(n)\end{aligned} \end{split}\]

Die N-Punkte DFT lässt sich also in zwei N/2-Punkte DFT zerlegen. Hierbei tritt jetzt das Problem auf, dass die Folgen \(U(n)\) und \(V(n)\) nur bis \(N/2\) definiert sind, da ja auch nur eine N/2 DFT durchgeführt wurde. Die Lösung für dieses Problem ist durch die Periodizität der DFT aber sehr einfach zu umgehen, da sich das Spektrum immer wiederholt.

Aber warum stellt es einen Vorteil dar, wenn man die DFT so zerlegen kann? Um eine diskrete Frequenz zu berechnen sind \(N\) komplexe Multiplikationen nötig. Dieser Schritt muss für alle diskreten Frequenzen durchgeführt werden. Die Berechnung des vollständigen Spektrums benötigt also \(N^2\) Multiplikationen. Teilen wir die Aufgabe in zwei Teilspektren benötigt man \(2\left(\frac{N}{2}\right)^2\) + \(N\) Multiplikationen für den Drehfaktor vor \(V(n)\). Im Vergleich ergeben sich für \(N = 8\) einmal 64 Multiplikationen und für die aufgeteilten Spektren 40 Multiplikationen. Der Schritt der Aufteilung kann nun solange wiederholt werden, bis die Folge nicht weiter aufgeteilt werden kann (\(N = 2\)). Zusätzlich können einige Multiplikationen vernachlässigt werden, da \(e^{j0} = 1\) ist. Eine Reduktion auf \(\frac{N}{2}\left( \text{ld}\left(\frac{N}{2}\right) \right)\) ist so möglich (ld = Logarithmus zur Basis 2, logarithmus dualis). Somit ergibt sich eine im rechenaufwand stark reduzierte DFT, die als Fast Fourier Transform (FFT) bekannt ist5.

5.4. Spezielle Signale und ihre Spektren

5.4.1. Spektrum für \(\delta(k)\)

Berechnet man die DTFT für den \(\delta\)-Impuls ergibt sich

(5.18)\[ X(e^{j \Omega}) = \sum_{k = -\infty}^{\infty} \delta(k)e^{-jk \Omega} =e^{-j0 \Omega} = 1~~~, \]

da der \(\delta\)-Impuls ausschließlich an der Stelle \(k = 0\) definiert ist. Der Betrag des Spektrums ist also eins für alle Frequenzen und die Phase ist null für alle Frequenzen.

5.4.2. Spektrum für \(\delta(k-k_0)\)

Der um \(k_0\) verschobene \(\delta\)-Impuls führt zu einem etwas anderem Spektrum

(5.19)\[ X(e^{j \Omega}) = \sum_{k = -\infty}^{\infty} \delta(k-k_0)e^{-jk \Omega} =e^{-jk_0 \Omega}~~~. \]

Das Spektrum ist im Betrag ebenfalls Eins für alle Frequenzen, aber die Phase des Signals wird linear abhängig von der Frequenz verändert, wenn ein \(\delta(k)\) ein System darstellt.

5.5. Weitere Fensterfunktionen und deren Eigenschaften

Wir haben gesehen, dass die DFT für eine zeitlich beschränkte Funktion auch als Multiplikation mit einer Fensterfunktion interpretiert werden kann. Dieses Fenster hatte einen deutlichen Einfluss auf das dargestellte Spektrum. Zur Beschreibung der Eigenschaften des Fensters im Frequenzbereich wird häufig die spektrale Auflösung des Maximums zu den 3 dB Punkten verwendet. Weiterhin ist die Höhe der nächsten Maxima (Betrag) interessant. Für das Rechteckfenster sind diese beiden Größen durch \(2pi/N\) und \(\approx 13\) dB gegeben. Etwas anders sieht dies bei anderen Fensterfunktionen aus (siehe Abbildung 5.10 bis Abbildung 5.16)

Interaktiv arbeiten

1. Starten des interaktiven Programms - Spektren_Fenster.py in jupyterbook/code/interactive_programs/

2. Mit den Buttons kann der Fenstertyp geändert und

3. mit Slidern die Fensterparameter gesteuert werden. Hier kann auch eine eigene Fensterfunktion designt werden.

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

import matplotlib
import numpy
from matplotlib import pyplot

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

matplotlib.style.use(f'{prefix}sv.mplstyle')

# create a rectengular window
rect_window = numpy.concatenate([[0]+[1]*30+[0]])
# and do zero padding
rect_window = numpy.concatenate([rect_window, [0]*1000])

spectrum = numpy.fft.fft(rect_window)
mid = numpy.floor(len(spectrum)/2)
# shift area from pi -> 2pi to -pi -> 0
spectrum = numpy.concatenate([spectrum[int(mid):], spectrum[:int(mid)]]) 
# dB maximum = 0dB
spectrum_abs = 20*numpy.log10(numpy.abs(spectrum)/numpy.abs(spectrum).max()) 
freqs_fft = numpy.linspace(-1, 1, len(spectrum_abs)) # freq bins, for plotting

fig, (ax_sample, ax_spectrum) = pyplot.subplots(1, 2)
ax_sample.plot(rect_window)
ax_sample.set(xlabel='Folgenndex k ->', ylabel='Amplitude x[k]', 
        xlim=[0, 31], title='Rechteck-Fenster im Frequenzbereich')

ax_spectrum.plot(freqs_fft, spectrum_abs)
ax_spectrum.set(xlabel='Frequenz rad/pi ', ylabel='Dämpfung in dB', 
        title='Rechteck-Fenster im Frequenzbereich')

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("RechteckWindow", fig, display=False)

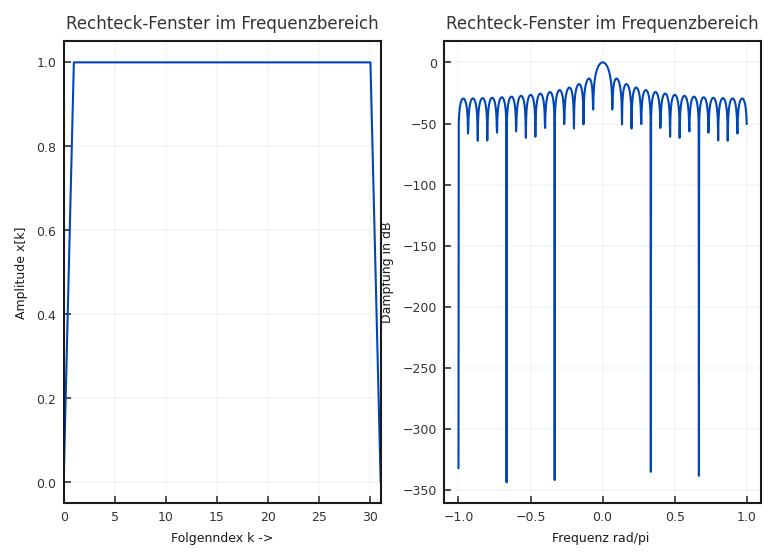
Fig. 5.10 Zeitliche und spektrale Eigenschaft des Rechteckfensters

Als Ursache für das Verschmieren im Frequenzbereich wurde die Faltung mit der Fensterfunktion genannt. Die Ursache im Zeitbereich hierfür war das abrupte Abschneiden, dass durch die angenommene zirkulare Wiederholung zu einem nicht-repräsentativen Ausschnitt führte. Deshalb ist eine Design-Idee für andere Fenster eine möglichst weiche Ausblendung zu den Rändern zu ermöglichen. Fenster die diese Eigenschaft besitzen können zum Beispiel durch Cosinusfunktionen realisiert werden.

Eine generalisierte Version ergibt sich dabei zu

(5.20)\[ w(k) = \alpha - \beta \cos(2\pi k /N) + \gamma \cos(4\pi k /N) \quad mit \quad 0\leq k < N \]

Durch Veränderung der drei Parameter \(\alpha, \beta, \gamma\) können die bekanntesten Fenster-Funktionen angegeben werden6.

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

import matplotlib
import numpy
from matplotlib import pyplot

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

N = 32
von_hann_window = [0]*N

for idx in range(N):
    von_hann_window[idx] = 0.5 - 0.5*numpy.cos(2*numpy.pi*idx/N)
von_hann_window = numpy.concatenate([von_hann_window, [0]*1000])
spectrum = numpy.fft.fft(von_hann_window)
mid = numpy.floor(len(spectrum)/2)
# shift area from pi -> 2pi to -pi -> 0
spectrum = numpy.concatenate([spectrum[int(mid):], spectrum[:int(mid)]]) 
# dB maximum = 0dB
spectrum_abs = 20*numpy.log10(numpy.abs(spectrum)/numpy.abs(spectrum).max()) 
freqs_fft = numpy.linspace(-1, 1, len(spectrum_abs)) # freq bins, for plotting
fig, (ax_sample, ax_spectrum) = pyplot.subplots(1, 2)
ax_sample.plot(von_hann_window)
ax_sample.set(xlabel='Folgenndex k ->', ylabel='Amplitude x[k]', xlim=[0, N-1],
        title='Von-Hann-Fenster im Zeitbereich')

ax_spectrum.plot(freqs_fft, spectrum_abs)
ax_spectrum.set(xlabel='Frequenz rad/pi ', ylabel='Dämpfung in dB', 
        title='Von-Hann-Fenster im Frequenzbereich')

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("HannWindow", fig, display=False)

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

import matplotlib
import numpy
from matplotlib import pyplot

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'
    
N = 32 # window length

# calculate window samples by sample
hamming_window = [0]*N 
for idx in range(N):
    hamming_window[idx] = 0.54 - 0.46*numpy.cos(2*numpy.pi*idx/N)

hamming_window = numpy.concatenate([hamming_window, [0]*100000]) # zero padding

spectrum = numpy.fft.fft(hamming_window)
mid = numpy.floor(len(spectrum)/2)
# shift area from pi -> 2pi to -pi -> 0
spectrum = numpy.concatenate([spectrum[int(mid):], spectrum[:int(mid)]]) 
# dB maximum = 0dB
spectrum_abs = 20*numpy.log10(numpy.abs(spectrum)/numpy.abs(spectrum).max()) 
freqs_fft = numpy.linspace(-1, 1, len(spectrum_abs)) # freq bins, for plotting

# time plot
fig, (ax_sample, ax_spectrum) = pyplot.subplots(1, 2)
ax_sample.plot(hamming_window)
ax_sample.set(xlabel='Folgenndex k ->', ylabel='Amplitude x[k]', xlim=[0, N-1],
        title='Hamming-Fenster im Zeitbereich')

# spectral plot
ax_spectrum.plot(freqs_fft, spectrum_abs)
ax_spectrum.set(xlabel='Frequenz rad/pi ', ylabel='Dämpfung in dB', 
        title='Hamming-Fenster im Frequenzbereich')

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("HammingWindow", fig, display=False)

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

import matplotlib
import numpy
from matplotlib import pyplot

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

N = 32 # window length

# calculate window samples by sample
blackman_window = [0]*N
for idx in range(N):
    blackman_window[idx] = 0.42 - 0.5*numpy.cos(2*numpy.pi*idx/N) + \
            0.08*numpy.cos(4*numpy.pi*idx/N)
blackman_window = numpy.concatenate([blackman_window, [0]*1000])


spectrum = numpy.fft.fft(blackman_window)
mid = numpy.floor(len(spectrum)/2)
# shift area from pi -> 2pi to -pi -> 0
spectrum = numpy.concatenate([spectrum[int(mid):], spectrum[:int(mid)]]) 
# dB maximum = 0dB
spectrum_abs = 20*numpy.log10(numpy.abs(spectrum)/numpy.abs(spectrum).max()) 
freqs_fft = numpy.linspace(-1, 1, len(spectrum_abs)) # freq bins, for plotting
fig, (ax_sample, ax_spectrum) = pyplot.subplots(1, 2)

# time plot
ax_sample.plot(blackman_window)
ax_sample.set(xlabel='Folgenndex k ->', ylabel='Amplitude x[k]', 
        xlim=[0, N-1], title='Blackman-Fenster im Zeitbereich')

# spectral plot
ax_spectrum.plot(freqs_fft, spectrum_abs)
ax_spectrum.set(xlabel='Frequenz rad/pi ', ylabel='Dämpfung in dB', 
        title='Blackman-Fenster im Frequenzbereich')

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("BlackmanWindow", fig, display=False)

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

import matplotlib
import numpy
from scipy import signal
from matplotlib import pyplot

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

N = 32 # window length

# create window in time domains
dolph_cheb_win = signal.windows.chebwin(N, at=40)
dolph_cheb_win = numpy.concatenate([dolph_cheb_win, [0]*1000])

spectrum = numpy.fft.fft(dolph_cheb_win)
mid = numpy.floor(len(spectrum)/2)
# shift area from pi -> 2pi to -pi -> 0
spectrum = numpy.concatenate([spectrum[int(mid):], spectrum[:int(mid)]]) 
# dB maximum = 0dB
spectrum_abs = 20*numpy.log10(numpy.abs(spectrum)/numpy.abs(spectrum).max()) 
freqs_fft = numpy.linspace(-1, 1, len(spectrum_abs)) # freq bins, for plotting

fig, (ax_sample, ax_spectrum) = pyplot.subplots(1, 2)
ax_sample.plot(dolph_cheb_win)
ax_sample.set(xlabel='Folgenndex k ->', ylabel='Amplitude x[k]', 
        xlim=[0, N-1], title='Dolph-Tschebyscheff-Fenster im Zeitbereich')

ax_spectrum.plot(freqs_fft, spectrum_abs)
ax_spectrum.set(xlabel='Frequenz rad/pi ', ylabel='Dämpfung in dB', 
        title='Dolph-Tschebyscheff-Fenster im Frequenzbereich')

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("ChebWindow", fig, display=False)

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

import matplotlib
import numpy
from matplotlib import pyplot

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

N = 32 # window length

# create windows in time domain
k4_window = numpy.kaiser(N, 4)
k2_window = numpy.kaiser(N, 2)
# zero pad
k4_window = numpy.concatenate([k4_window, [0]*1000])
k2_window = numpy.concatenate([k2_window, [0]*1000])


spectrum_k4 = numpy.fft.fft(k4_window)
spectrum_k2 = numpy.fft.fft(k2_window)

mid = numpy.floor(len(spectrum_k4)/2)

# shift pi -> 2*pi to -pi -> 0
spectrum_k4 = numpy.concatenate([spectrum_k4[int(mid):], spectrum_k4[:int(mid)]])
spectrum_k2 = numpy.concatenate([spectrum_k2[int(mid):], spectrum_k2[:int(mid)]])
# dB normalized to maximum amplitude=0dB
spectrum_k4_abs = 20*numpy.log10(
        numpy.abs(spectrum_k4)/numpy.abs(spectrum_k4).max())
spectrum_k2_abs = 20*numpy.log10(
        numpy.abs(spectrum_k2)/numpy.abs(spectrum_k2).max())
# frequency bins, for plotting
freqs_fft_k4 = numpy.linspace(-1, 1, len(spectrum_k4_abs))
freqs_fft_k2 = numpy.linspace(-1, 1, len(spectrum_k2_abs))

# time and frequency domain plots of beta = 4
fig1, (ax_sample_k4, ax_spectrum_k4) = pyplot.subplots(1, 2)
ax_sample_k4.plot(k4_window)
ax_spectrum_k4.plot(freqs_fft_k4, spectrum_k4_abs)
ax_sample_k4.set(xlabel='Folgenndex k ->', ylabel='Amplitude x[k]', 
        xlim=[0, N-1], title='Kaiser-Fenster (alpha = 4) im Zeitbereich')
ax_spectrum_k4.set(xlabel='Frequenz rad/pi ', ylabel='Dämpfung in dB', 
        title='Kaiser-Fenster (alpha = 4) im Frequenzbereich')

# time and frequency domain plots of beta = 2 
fig2, (ax_sample_k2, ax_spectrum_k2) = pyplot.subplots(1, 2)
ax_sample_k2.plot(k2_window)
ax_spectrum_k2.plot(freqs_fft_k2, spectrum_k2_abs)
ax_sample_k2.set(xlabel='Folgenndex k ->', ylabel='Amplitude x[k]', 
        xlim=[0, N-1], title='Kaiser-Fenster (alpha = 2) im Zeitbereich')
ax_spectrum_k2.set(xlabel='Frequenz rad/pi ', ylabel='Dämpfung in dB', 
        title='Kaiser-Fenster (alpha = 2) im Frequenzbereich')

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("KaiserWindow-a4", fig1, display=False)
glue("KaiserWindow-a2", fig2, display=False)

von Hann

• von Hann-Fenster (oft fälschlich Hanning): Für das Hann-Fenster ist \(\alpha = \beta = 0{,}5\) und \(\gamma = 0\). Daraus ergibt sich im Frequenzbereich ein etwas breiteres Hauptmaxima \(4\pi/N\). Die Nebenmaxima sind dafür im Gegensatz zum Rechteck-Fenster sehr viel stärker bedämpft.

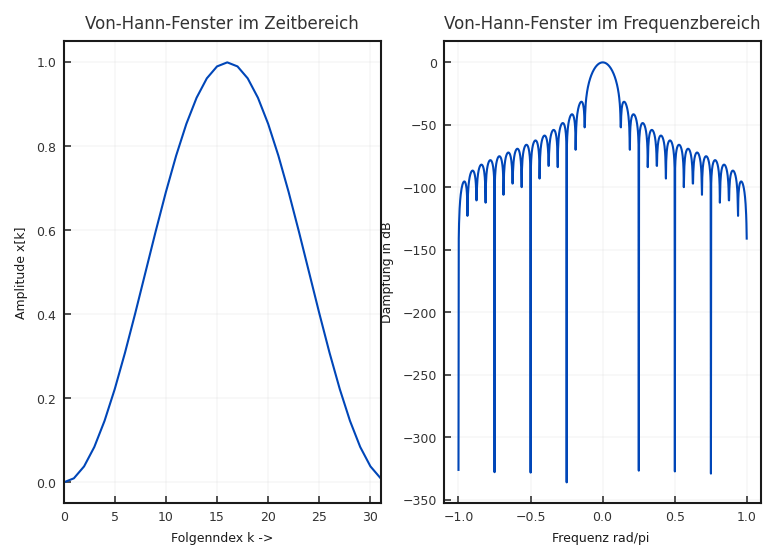
Fig. 5.11 Zeitliche und spektrale Eigenschaft des von Hann-Fensters

Hamming

• Hamming-Fenster: Für das Hamming-Fenster ist \(\alpha = 0{,}54\), \(\beta = 0{,}46\) und \(\gamma = 0\). Das Design-Ziel des Hamming-Fenster ist das erste Nebenmaxima möglichst optimal zu unterdrücken. Dafür geht aber insgesamt eine schlechtere Dämpfung der anderen Nebenmaxima einher. Die Verbreiterung entspricht der des Hann-Fensters \(4\pi/N\).

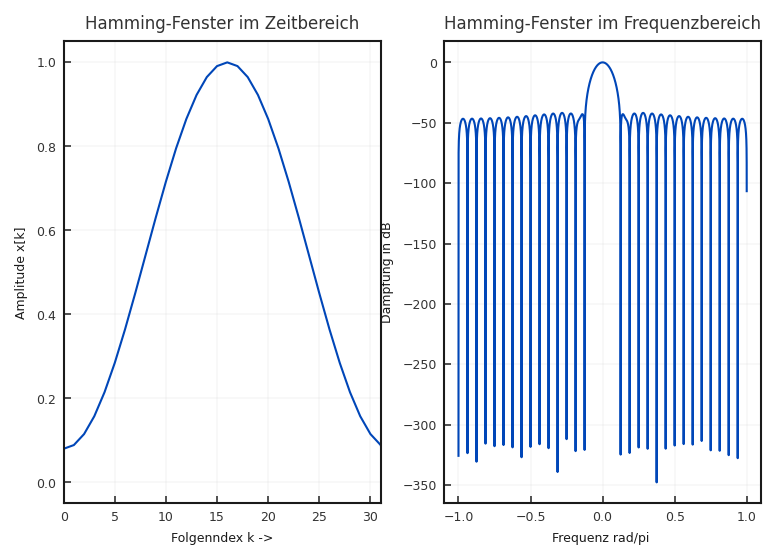
Fig. 5.12 Zeitliche und spektrale Eigenschaft des Hamming-Fensters

Blackman

• Blackman-Fenster: Für das Blackman-Fenster ist \(\alpha = 0{,}42\), \(\beta = 0{,}5\) und \(\gamma = 0{,}08\). Dieses Fenster hat eine deutlich breitere Hauptkeule \(6\pi/N\), aber die Dämpfung der Nebenmaxima und der Abfall der weiteren Nebenmaxima ist sehr hoch.

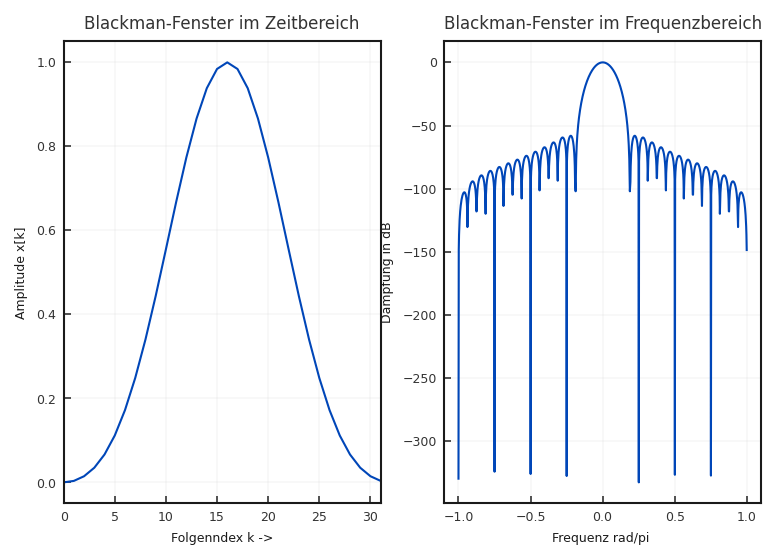
Fig. 5.13 Zeitliche und spektrale Eigenschaft des Blackman-Fensters

Dolph-Tschebyscheff

• Dolph-Tschebyscheff-Fenster: Im Gegensatz zu den anderen Fenstern in dasDolph-Tschebyscheff-Fenster parametrisierbar. Bei einer vorgegebenen Fensterlänge \(N\) kann die Absenkung der Nebenzipfel angegeben werden. Dieser Wert wird für alle Nebenzipfel gleichmäßig erreicht. Die Breite der Hauptkeule wird gleichzeitig optimal klein für eine gegebene Fensterlänge \(N\). Siehe auch chebwin in Matlab.

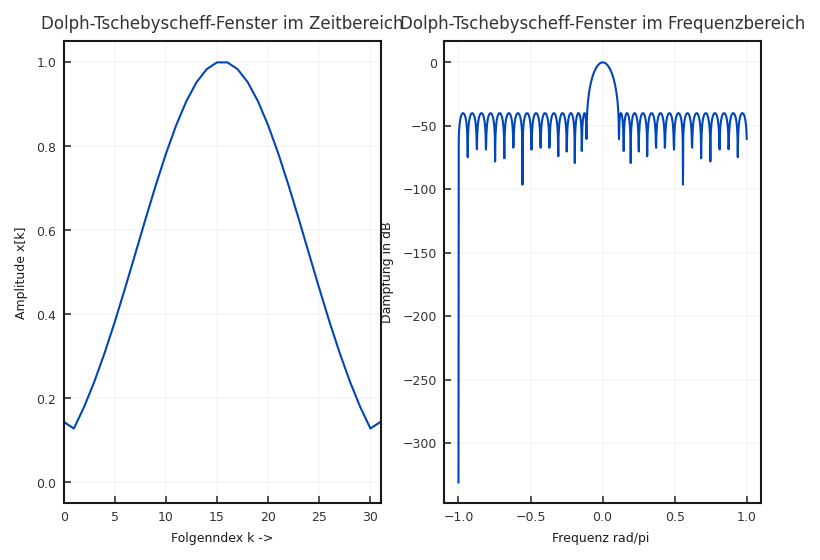
Fig. 5.14 Zeitliche und spektrale Eigenschaft des Dolph-Tschebyscheff-Fensters

Kaiser-Fester

• Kaiser-Fenster: Auch das Kaiser-Fenster ist mit Hilfe des Parameters \(\alpha\) veränderlich. Es basiert auf der Form

(5.21)\[\begin{split} w(k,\alpha) = \left\{\begin{array}{c} \frac{I_0\left(\alpha \sqrt{1-(k/N)^2}\right)}{I_0 (\alpha)} \quad mit \quad 0\leq k < N\\ 0 \quad \quad \mbox{sonst} \\ \end{array} \right. \end{split}\]

wobei \(I_0\) die modifizierte Bessel-Funktion nullter Ordnung darstellt.

Abbildung 5.15 und Abbildung 5.16 zeigen für unterschiedliche \(\alpha\) den zeitlichen Verlauf und die dazugehörigen spektralen Eigenschaften.

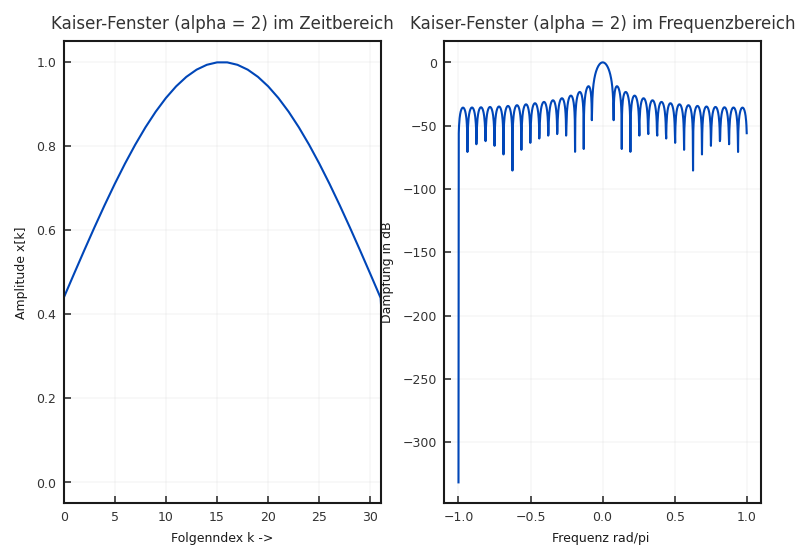
Fig. 5.15 Zeitliche und spektrale Eigenschaft des Kaiser-Fensters mit \(\alpha =\) 2.

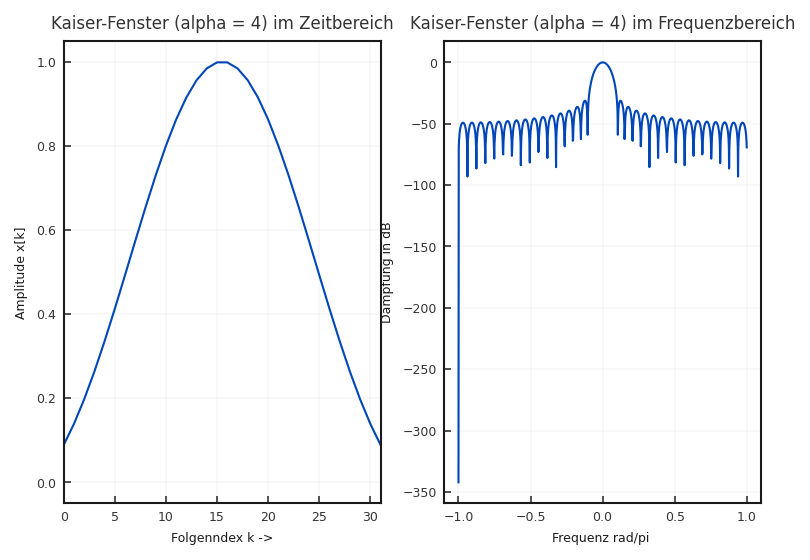
Fig. 5.16 Zeitliche und spektrale Eigenschaft des Kaiser-Fensters mit \(\alpha =\) 4.

---

2

\[1+x + x^2 + \cdots + x^{N-1} = \frac{1-x^N}{1-x}\]

3

Es enstehen keine genaueren Spektralwerte gegenüber der kurzen Folge. Die Werte bei der höheren Frequenzauflösung könnten auch aus einer Interpolation des Spektrums mit geringrer Auflösung gewonnen werden.

5

In Matlab wird die DFT durch die Funktion FFT aufgerufen.

6

Bei der Darstellung wurden die jeweiligen Übertragungsfunktionen auf ihr Maximum normiert, so dass sich immer ein Hauptmaxima mit 0dB ergibt.