3. Systeme#

Betrachtet man die typische Nachrichtenübertragungskette, so ist das Bindeglied zwischen Quelle und Senke der Kanal. Eine andere, allgmeinere Bezeichnung für den Kanal ist der Begriff System. Ganz allgemein kann davon gesprochen werden, dass ein System verschiedene (unterschiedliche) Signale miteinander verknüpft und Beziehungen herstellt. Abbildung 3.1 zeigt eine allgemeine Verknüpfung von Signalen.

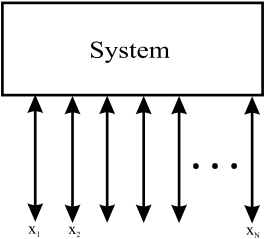
_images/SystemAllgemein.png

Fig. 3.1 Veranschaulichung eines allgemeinen Systems, dass Signale miteinander verknüpft.#

In den meisten Fällen kann diese sehr allgemeine Verknüpfung spezifiziert werden. Insbesondere haben wir häufig Eingangssignale auf die das System reagiert und die daraus resultierenden Ausgangssignale (siehe Abbildung 3.2).

_images/SystemEinAus.png

Fig. 3.2 Veranschaulichung eines allgemeinen Systems, mit Signalen die als Ein- und Ausgangssignale festliegen.#

Durch diese sehr allgemeine Formulierung des Systembegriffs wird auch deutlich, warum die Systemtheorie eine zentraler Punkt vieler wissenschaftlicher Richtungen ist. Einige weitere Beispiele:

  • HiFi-Verstärker: Ein System mit mehreren Eingängen und wenigen (meist zwei) Ausgängen

  • Der Mensch: Ein sehr komplexes System mit vielen Eingängen (Sinnesorganen) und vielen Ausgängen (Muskeln)

  • Computer: Viele Eingänge und Ausgänge

  • Ihr Beispiel

3.1. Eigenschaften und Klassifikation von Systemen#

Bei der Klassifikation der Systeme können wir zunächst die meisten Punkte, die wir für Signale erarbeitet haben, ebenfalls anwenden.

3.1.1. Wert- und Definitionsbereich#

Da wären zunächst die Frage, ob es sich bei dem betrachteten System um ein analoges (wertkontinuierlich und zeitkontinuierlich) oder um ein digitales (zeit- und wertdiskret) System handelt. In den nächsten Abschnitten werden wir uns zunächst nur mit digitalen Systemen beschäftigen.

Die Klassifikation erfolgt also nach:

Wichtig

analoges System vs. digitales System

3.1.2. Kanalanzahl#

Die Kanalanzahl ist ebenfalls eine Möglichkeit ein System zu beschreiben und zu klassifizieren, wobei als Besonderheit zu beachten ist, dass Systeme auch die Kanalanzahl verändern können. So kann z.B. ein Monosignal (Gesang) auf zwei Kanäle aufgespalten werden um so eine Positionierung in einem Stereosignal zu ermöglichen.

_images/PanAllgemein.png

Fig. 3.3 Beispiel eines Systems mit einem Eingang und zwei Ausgängen.#

Wir können also Systeme nach der Kanalzahl der Ein- und Ausgänge klassifizieren.

Wichtig

Einkanalig vs. Mehrkanalig

Der allgemeinste Fall des mehrkanaligen Ein- und Ausgangs wird als MIMO-System (Multiple Input Multiple Output) bezeichnet.

3.1.3. Dimensionalität#

So wie es ein- und mehrdimensionale Signale gibt, so können auch Systeme in mehreren Dimensionen wirken. Ein einfaches Beispiel wäre ein bildveränderndes System, dass natürlich zwei-dimensional arbeiten müsste.

Wichtig

eindimensional vs. mehrdimensional

3.1.4. Rekursivität#

Eine Eigenschaft, die wir bisher nicht mit Signalen erarbeitet haben, ist die Frage, ob das System den eigenen Ausgang als weiteren Eingang betrachtet. Abbildung 3.4 zeigt ein System dass sein Ausgangssignal auf den Eingang zurückführt. Ein solches System bezeichnen wir als rekursives System.

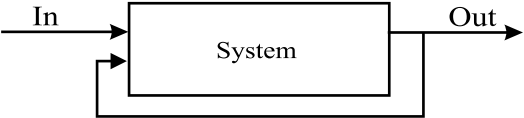
_images/RekursivSystem.png

Fig. 3.4 Allgemeines Blockdiagramm eines einkanaligen rekursiven Systems.#

Da es auch nicht-rekursive Systeme gibt, können wir folgende Klassifikation einführen

Wichtig

rekursive vs. nicht-rekursive (transversale) Systeme

Um die Wichtigkeit von rekursiven Systemen zu verdeutlichen, nehmen wir einmal an, wir bräuchten ständig die Summe von mehreren vergangenen Messwerten (oder ein Beispiel aus der Praxis ist der 30-Tage Durchschnitt bei der DAX-Analyse). Wir können diese Summe immer wieder durch

\[ y(k) = \sum_{m=0}^{M-1}x(k-m) \]

berechnen. Die Anzahl der Messwerte, die wir verwenden ist durch \(M\) symbolisiert.

Betrachtet man diese Rechenvorschrift, so fällt auf, dass bestimmte Anteile immer wieder summiert werden und immer nur ein neuer Wert hinzukommt und ein alter Wert aus der Summation herausfällt. Dies ist in Abbildung 3.5 genauer gezeigt.

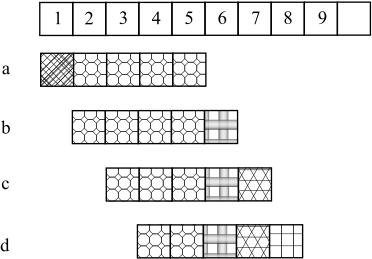
_images/DatenwerteRekursion.png

Fig. 3.5 Erläuterung zur Anwendung der Rekursion. Bei einer Summenbildung über die jeweiligen Zeilen (a-d) sind die Summen zwischen a und b die achteckig gefüllten Elemente bereits für a addiert worden. Man kann deshalb bei b durch Subtraktion des gestrichelten ersten Elements und Addition des Elements mit Kreuz direkt die neue Summe berechnen.#

Man könnte also das Ausgangssignal des Systems auch durch

\[ \label{eq:RekursionsBsp} y(k) = y(k-1) + x(k) - x(k-M). \]

berechnen. Es ist also möglich die Rechenleistung durch rekursive Berechnungen zu verringern.

3.1.5. Gedächtnis#

Bei der Rekursion haben wir gesehen, dass durch Speicherung der Eingangsfolge und Speicherung des letzten Ausgangswertes sehr einfach bestimmte Systeme realisiert werden können. Systeme die Speicherelemente beinhalten werden gedächtnisbehaftet genannt. Systeme bei denen der Ausgang nur von den Eingangssignalen, aber nicht von dem vorherigen Zustand abhängig ist, sind gedächtnislos. Ein Beispiel für ein gedächtnisloses System ist die Funktion \(y(k) = x^2(k)\).

Wichtig

gedächtnisbehaftet vs. gedächtnislos

Die Gedächtnislänge eines Systems ist durch die Möglichkeit der größten Signalverzögerung \(k_0\) vorgegeben. Diese kann im transversalen oder im rekursiven Zweig des Systems vorkommen. Der Hauptunterschied liegt im Einfluss des Gedächtnisses. Bei ausschließlich transversalen Systemen bestimmt die Gedächtnislänge die Einflusslänge. Für rekursive Systeme ist die Einflusslänge bis auf sehr wenige Ausnahmen unabhängig von der Gedächtnislänge unendlich.

3.1.6. Kausalität#

Die Kausalität ist für Systeme eine sehr wichtige Eigenschaft. Nur bei kausalen Systemen ist die Ursache (Eingangssignal) zeitlich immer vor der Wirkung (Ausgangssignal). Anders ausgedrückt das Ausgangssignal darf nur von dem jetztigen Eingang und vorherigen Eingangswerten abhängen, damit ein kausales System vorliegt. Mathematisch kann dies durch

\[ y(k_0) = f\{x(k\leq k_0)\} \]

ausgedrückt werden.

3.1.7. Stabilität#

Eine andere sehr wichtige Eigenschaft für Systeme ist ihre Stabilität. Stabile Systeme zeichnen sich dadurch aus, dass sie auf ein begrenztes Eingangssignal mit einem begrenzten Ausgangssignal reagieren (BIBO-Stabilität, Bounded Input Bounded Output). Mathematisch muss folgendes als notwendige Bedingung gelten:

\[ \mbox{wenn} \quad |x(k)| < \infty \quad \Rightarrow \quad |f\{x(k)\}| < \infty \]

Beispiel

Sind die folgenden Systeme stabil?

  • \(y(k) = x^2(k)\):
    Das System ist stabil, da alle möglichen Eingangswerte für x(k), die kleiner als \(|\infty|\) sind, wieder auf Werte führen die kleiner als \(\infty\) sind

  • \(y(k) = \log(x(k))\):
    Für \(x(k) = 0\) ist \(y(k) = -\infty\). Somit ist das System instabil.

3.2. LTI-Systeme#

Eine besondere Klasse an Systemen stellen die linearen, zeitinvarianten (LTI, Linear and Time-Invariant) Systeme dar. Die beiden Begriffe Linearität und Zeitinvarianz werden im weiteren als Systemeigenschaften genauer beschrieben

3.2.1. Linearität#

Lineare Systeme zeichnen sich dadurch aus, dass das sog. Superpositionsprinzip (Überlagerungsprinzip) gilt. Dies bedeutet, dass die additive Überlagerung der gewichteten Eingangssignale und die Verknüpfung mit dem System genau zu dem gleichen Ergebnis führt, wie die gewichtete additive Überlagerung der einzelnen Signale am Ausgang des linearen Systems. Mathematisch ausgedrückt durch

\[\begin{split} \label{eq:Linearitaet} f\{a_1 x_1(k) + a_2 x_2(k) + \cdots + a_N x_N(k)\} = \\ a_1 f\{x_1(k)\} + a_2 f\{x_2(k)\} + \cdots + a_N f\{x_N(k)\}~~~, \end{split}\]

wobei \(f\{\cdot\}\) die Systemfunktion darstellt, \(a_i\) die linearen Gewichte und \(x_i(k)\) die Eingangssignale. Abbildung 3.6 verdeutlicht den Zusammenhang. Bei LTI-Systemen kann das System \(H\) vor den Summationspunkt und vor den linearen Gewichten \(a_1\) und \(a_2\) verschoben werden.

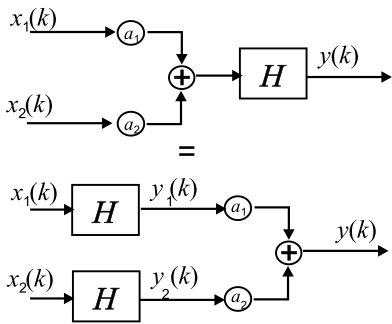
_images/LinearitaetErklaerung.png

Fig. 3.6 Linearität bildlich erklärt#

Beispiel

Als Beispiel betrachten wir das System

\[ y(k) = 2x(k) + 3x(k-1) \]

Der Ausgang der einzelnen Eingangssignale \(x_1(k)\) und \(x_2(k)\) gewichtet ergeben

\[\begin{split} \begin{aligned} y_1(k) &= & (2x_1(k) + 3x_1(k-1))\\ y_2(k) &= & (2x_2(k) + 3x_2(k-1))\\\end{aligned} \end{split}\]

Der Ausgang ergibt sich zu

\[ \label{eq:Ausgangdirekt} y(k) = a_1 y_1(k)+ a_2 y_2(k). \]

und somit

(3.1)#\[ y(k) = 2 a_1 x_1(k) + 3 a_1 x_1(k-1)+ 2 a_2 x_2(k) + 3 a_2 x_2(k-1). \]

Ein gemischtes und gewichtetes Eingangssignal ist gegeben durch

\[ x_\text{mix} = a_1 x_1(k) + a_2 x_2(k) \]

und das Ausgangssignal des System durch

\[\begin{split} \begin{aligned} y(k) &=& 2x_\text{mix}(k) + 3x_\text{mix}(k-1)\\\nonumber & = & 2(a_1 x_1(k) + a_2 x_2(k)) + 3(a_1 x_1(k-1) + a_2 x_2(k-1))\\\nonumber & = & 2a_1x_1(k) + 2 a_2 x_2(k) + 3 a_1 x_1(k-1) + 3 a_2 x_2(k-1)\end{aligned} \end{split}\]

Dies ist im Vergleich zur Gleichung (3.1) identisch. Somit ist das System linear.

Als zweites System testen wir \(y(k) = x^2(k)\). Es ergeben sich folgende Ausgangssignale:

\[\begin{split} \begin{aligned} y_1(k) & = & x_1^2 (k)\\ y_2(k) & = & x_2^2 (k)\\ \Rightarrow y(k) &= &a_1 y_1(k) + a_2 y_2(k)\\ & = & a_1 x_1^2 (k) + a_2 x_2^2 (k)\end{aligned} \end{split}\]

bzw.

\[\begin{split} \begin{aligned} y(k) &= & x_\text{mix}^2 (k)\\ & = & \left( a_1 x_1 (k) + a_2 x_2 (k) \right)^2\\ & = & a_1^2 x_1^2 (k) + 2a_1 a_2 x_1(k) x_2(k) + a_2^2 x_2^2 (k)\end{aligned} \end{split}\]

Die beiden Ausgangssignale sind nicht identisch. Dieses System ist also nichtlinear.

3.2.2. Zeitinvarianz#

Von Zeitinvarianz spricht man, wenn das System seine Eigenschaften nicht zeitlich ändert. Eine bestimmmte Verzögerung \(k_0\) des Eingangssignal führt also im Ausgang zu einem um die selbe Zeit \(k_0\) verzögerten Ausgangssignal. Mathematisch ausgedrückt durch

\[ y(k) = f\{x(k) \} \quad \Rightarrow y(k-k_0) = f\{x(k-k_0) \} \]

mit \(k_0\) als Angabe der diskreten Verzögerungszeit.

Beispiel

Gegeben sind die beiden Systeme \(y(k) = 2x(k)\) und \(y(k) = x(2k)\). Sind die Systeme zeitinvariant oder nicht?

Der Test erfolgt zum einen über die zeitliche Verschiebung des Eingangssignals \(x(k)\). Es ergibt sich ein neues Eingangssignal \(x(k-k_0)\). Für dieses neue Eingangssignal ist der Ausgang \(y(k) = 2x(k-k_0)\). Zum anderen muss das Ausgangssignal des Originaleingangssignals verschoben werden. Es ergibt sich zunächst für den Ausgang \(y(k) = 2 x(k)\). Dieses Signal wird jetzt um \(k_0\) verschoben (Variablensubstitution \(k' = k-k_0\)). Der Ausgang ist also \(y(k') = y(k-k_0) = 2 x(k-k_0)\). Das System ist zeit-invariant.

Beim zweiten System ergibt sich am Ausgang durch die Verschiebung des Eingangssignals \(y(k) = x(2k-k_0)\). Betrachtet man aber den um \(k_0\) verschobenen Ausgang ergibt sich durch die Variablensubstitution \(y(k-k_0) = x(2k-2k_0)\). Dieses System ist also zeitvariant.

3.2.3. Beschreibung durch Differenzengleichungen#

LTI-Systeme lassen sich stets durch Differenzengleichungen mit festen Koeffizienten ausdrücken. Dies ist für nichtrekursive Systeme mit den Beispielen des Abschnittes über Linearität auch leicht nachvollziehbar. Gleichzeitig gilt die selbe Linearitätsbeziehung auch für den Ausgang des Systems. Betrachtet man nun ein rekursives System, so kommen als neue Terme nur vergangene Systemantworten mit linearen Faktoren gewichtet (multipliziert) hinzu. Damit sind auch alle durch

\[ \sum_{i = 0}^{N} a_i y(k-i) = \sum_{j = 0}^{M}b_j x(k-j) \]

aufgebauten rekursiven Systeme linear.

Um nun nur den Ausgang des Systems zu betrachten, wird vereinbart, dass \(a_0 = 1\) ist 1. Für den Ausgang eines kausalen Systems gilt dann

\[ y(k) = -\sum_{i = 1}^{N}a_i y(k-i) + \sum_{j = 0}^{M}b_j~~~. x(k-j) \]

Um zu wissen, welche Folge \(y(k)\) am Ausgang herauskommt, ist es notwendig den aktuellen und die vergangenen Eingangssignale \(x(k)\) zu kennen. Zusätzlich muss aber auch bekannt sein, wie die inneren Zustände des Systems aussehen. Es müssen also die vorherigen Ausgangswerte bekannt sein, um die vollständige Beschreibung zu gewährleisten. Häufig wird vereinfacht angenommen, dass das System in Ruhe war und deshalb gilt

\[ y(k-i) = 0 \qquad \forall \qquad i>0~~~. \]

3.2.3.1. Einführung der Systemantwort auf die Delta-Impulsfolge#

Die Systemantwort auf die Delta-Impulsfolge \(\delta(k)\) wird als Impulsantwort \(h(k)\) bezeichnet und charakterisiert ein LTI-System vollständig. Für nicht-rekursive Systeme mit einer endlichen Anzahl von Koeffizienten, also \(M< \infty\), ist die Impulsantwort endlich. Deshalb werden diese Systeme auch als Finite Impulse Response (FIR)-Systeme bezeichnet. Bei rekursiven Systeme gilt dies im allgemeinen nicht. Diese Systeme werden deshalb als Infinite Impulse Response (IIR)-Systeme bezeichnet.

Beispiel

Nehmen wir an, wir suchen die Impulsantwort des LTI-Systems

\[y(k) = r_0 x(k) + r_1 x(k-1) - r_2 x(k-2)~~~.\]

Errechnet man nun den Ausgang für alle \(k\) und setzt jeweils für \(x(k)\) die Impulsfolge ein, so ergibt sich die Impulsantwort2

\[h(k) = [r_0 \,\, r_1 \,\, -r_2] \qquad \text{für} \qquad 0 \leq k \leq 2~~~.\]

Das betrachtete System war ein FIR-System. Ganz allgemein ergibt sich für FIR-Systeme immer, dass \(h(k) = b_k\) ist.

Für IIR-Systeme ist die Berechnung der Impulsantwort nicht so trivial. Betrachten wir das System

\[ y(k) = \alpha y(k-1) + \beta x(k)~~~. \]

Als Eingangssignal nutzen wir erneut \(x(k)= \delta(k)\). Die Ausgangsfolge für alle \(k\) berechnet ergibt

\[ h(k) = [\beta \,\, \alpha \beta \,\, \alpha \alpha \beta \,\, \cdots \,\, \alpha^{k}\beta]~~~. \]

Die Impulsantwort endet nicht.

Für viele Probleme reicht es aber aus, die Impulsantwort nur so weit zu betrachten, wie sich noch signifikante Werte ergeben. Signifikant kann dabei zum Beispiel bedeuten, dass die Werte von \(h(k)\) größer als der millionste Teil des maximalen Wertes von \(h(k)\) sind.

Wichtig

Die Impulsantwort eines Systems ist der Ausgang des Systems, wenn die Eingangsfolge die Delta-Impulsfolge ist. Die Impulsantwort beschreibt ein LTI-System vollständig

Nichtrekursive Systeme haben eine endliche Impulsantwort. Sie werden als FIR-Systeme bezeichnet.

3.2.4. Faltung als Verknüpfung von LTI-Systemen und Signalen#

Bisher haben wir nur gesehen, wie die Eingangssignale durch die Differenzengleichung zum Ausgangssignal werden. Es gibt aber eine allgemeinere Vorschrift, die direkt mit der Impulsantwort zusammen hängt.

Zur Veranschaulichung wird zunächst ein einfaches Beispiel berechnet. Das Eingangssignal ist durch zwei Werte gegeben, wir nehmen an \(x(0)= 0{,}5\) und \(x(1) = 1{,}5\). Das System ist durch

\[y(k) = -0{,}25x(k) + 0{,}5x(k-1)\]

definiert. Wie lautet die Ausgangssfolge? Man könnte jetzt einfach die verschiedenen Zeitpunkte \(k\) annehmen und das Ergebnis direkt hinschreiben. In Tabellenform wäre das Ergebnis:

import pandas

df = pandas.DataFrame(data = {'k':[0, 1, 2, 3], 'x(k)':[0.5, 1.5, 0, 0],'x(k-1)':[0, 0.5, 1.5, 0],'y(k)':[-0.125, -0.125, 0.75, 0]})
df = df.set_index('k')
df
x(k) x(k-1) y(k)
k
0 0.5 0.0 -0.125
1 1.5 0.5 -0.125
2 0.0 1.5 0.750
3 0.0 0.0 0.000

Für dieses einfache Beispiel ist das noch leicht möglich, bei längeren Folgen wäre diese Lösung unpraktisch. Statt dessen versuchen wir einen allgemeineren Lösungsweg zu finden. Die Eingangsfolge \(x(k)\) lässt sich für alle \(k\) mit Hilfe der delta-Folge \(\delta(k)\) durch

\[ \label{eq:diracinput} x(k) = 0{,}5 \delta(k) + 1{,}5 \delta(k-1) \]

vollständig beschreiben.

Mit dem Gesetz der Linearität und dem Wissen der Impulsantwort \(h(k) = [-0{,}25 \:\, 0{,}5]\), ergibt sich die Antwort für \(y(k)\) aus der Summe der gewichteten und verschobenen Impulsantworten, da jede der delta-Folgen die Impulsantwort als Systemantwort hervor ruft.

Allgemeiner lässt sich sagen, jedes diskrete Eingangssignal lässt sich in viele kleine Einzelimpulse zerlegen. Wir haben es also immer mit einer gewichteten Summe von Delta-Impulsfolgen zu tun. Aus dem letzten Abschnitt haben wir kennengelernt, dass die Impulsantwort ein LTI-System vollständig beschreibt. Außerdem gilt für LTI-Systeme das Superpositionsprinzip. Das Ausgangssignal eines LTI-Systems kann deshalb durch eine mit linearen Koeffizienten gewichtete Addition der zeitlich verschobenen Impulsantwort berechnet werden.

Um dies zu veranschaulichen, ist in Abbildung 3.7 diese Zerlegung für ein Beispiel durchgeführt. Bild a) zeigt die Eingangssfolge \(x(k) = [1\,\, 0{,}5 \,\, 1]\) , Bild b) das System \(h = [0{,}5 \,\,\, 0{,}75 \; 1]\). Zerlegt man nun die Eingangsfolge in drei Einzelimpulse ergeben sich die drei Bilder c,e,g. Jeder dieser Einzelimpulse erzeugt eine verschobene und gewichtete Version der Impulsantwort (Bild d,f,h). Das Ausgangssignal (i) ergibt sich schlussendlich aus der Summe dieser Ausgangssignale.

# -*- coding: utf-8 -*-
#-------------------------------------------------------------------------------
# Demoscript for "Signalverarbeitung 1"
#
# Version: 1.0   17.02.2022
# 
# This software is released as public domain under CC0 1.0
# https://creativecommons.org/publicdomain/zero/1.0/
#-------------------------------------------------------------------------------

import matplotlib
import numpy
from matplotlib import pyplot

# this script only consist of plotting predifinded vectors
# and the convolution of them with the system

# determine where we're running from and set paths accordingly
try: 
    if get_ipython().__class__.__name__ == 'ZMQInteractiveShell':
        prefix = ''
except:
    prefix = '../../'

matplotlib.style.use(f'{prefix}sv.mplstyle')

index = [0, 1, 2, 3, 4, 5, 6]
x = [1, 0.5, 1]
x0 = [1, 0, 0]
x1 = [0, 0.5, 0]
x2 = [0, 0, 1]
system = [0.5, 0.75, 1]

fig, ((ax_input, ax_system),(ax_x0, ax_yx0),(ax_x1, ax_yx1),(ax_x2, ax_yx2),
        (ax_empty, ax_sum)) = pyplot.subplots(5, 2, sharex='all', sharey='all')


ax_input.stem(x + [0, 0], use_line_collection=True)
ax_input.set(xlabel='Folgenindex k ->', ylabel='Amplitude x[k]', 
        title='a) Inputsignal', xlim=[0, 6], ylim=[0, 2])

ax_system.stem(system + [0, 0], use_line_collection=True)
ax_system.set(xlabel='Folgenindex k ->', ylabel='Amplitude x[k]', 
        title='b) System', xlim=[0, 6], ylim=[0, 2])

ax_x0.stem(x0, use_line_collection=True)
ax_x0.set(xlabel='Folgenindex k ->', ylabel='Amplitude x[k]', 
        title='c) Input bei x[0]', xlim=[0, 6], ylim=[0, 2])

y_x_0 = numpy.convolve(x0, system)
ax_yx0.stem(y_x_0, use_line_collection=True)
ax_yx0.set(xlabel='Folgenindex k ->', ylabel='Amplitude x[k]', 
        title='d) Systemantwort für x[0]', xlim=[0, 6], ylim=[0, 2])


ax_x1.stem(x1, use_line_collection=True)
ax_x1.set(xlabel='Folgenindex k ->', ylabel='Amplitude x[k]', 
        title='e) Input bei x[1]', xlim=[0, 6], ylim=[0, 2])

y_x_1 = numpy.convolve(x1, system)
ax_yx1.stem(y_x_1, use_line_collection=True)
ax_yx1.set(xlabel='Folgenindex k ->', ylabel='Amplitude x[k]', 
        title='f) Systemantwort für x[1]', xlim=[0, 6], ylim=[0, 2])


ax_x2.stem(x2, use_line_collection=True)
ax_x2.set(xlabel='Folgenindex k ->', ylabel='Amplitude x[k]', 
        title='g) Input bei x[2]', xlim=[0, 6], ylim=[0, 2])

y_x_2 = numpy.convolve(x2, system)
ax_yx2.stem(y_x_2, use_line_collection=True)
ax_yx2.set(xlabel='Folgenindex k ->', ylabel='Amplitude x[k]', 
        title='h) Systemantwort für x[2]', xlim=[0, 6], ylim=[0, 2])

conv_sum = numpy.convolve(x, system)
ax_sum.stem(conv_sum, use_line_collection=True)
ax_sum.set(xlabel='Folgenindex k ->', ylabel='Amplitude x[k]', 
        title='i) Systemantwort für Inputsignal', xlim=[0, 6], ylim=[0, 2])
pyplot.tight_layout()

pyplot.show()

# glue this figure to paste it later (no effect outside of MyST NB)
from myst_nb import glue
glue("FaltungErklaerung", fig, display=False)
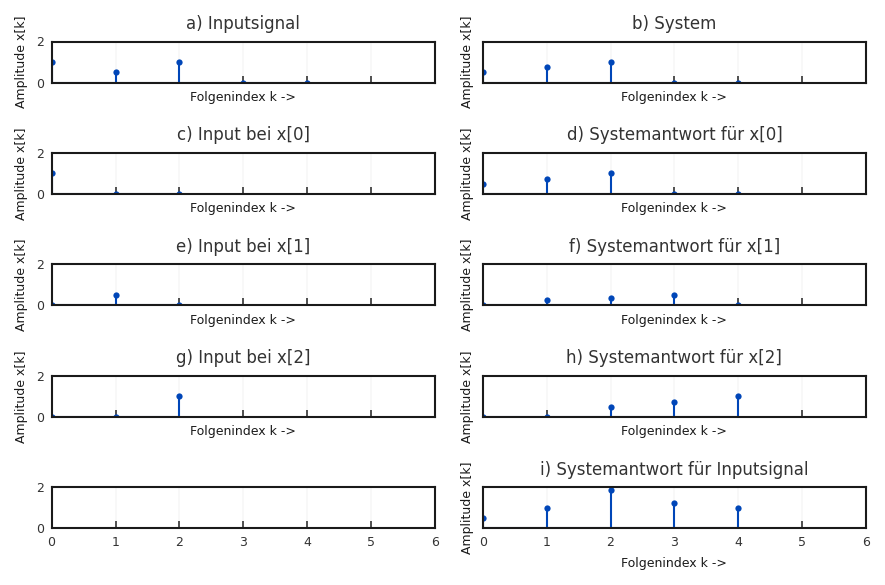
_images/systeme_11_1.png

Fig. 3.7 Einfache grafische Erklärung der Faltung.#

Allgemein und mathematisch wird dies durch

\[ y(k) = \sum_{\kappa = -\infty}^{\infty} h(\kappa) x(k-\kappa) \]

ausgedrückt. Diese Summe wird als Symbol durch \(\ast\) dargestellt und als Faltungsumme bezeichnet:

\[\begin{split} \begin{aligned} y(k) &=& \sum_{\kappa = -\infty}^{\infty} h(\kappa) x(k-\kappa)\\ & = & h(k) \ast x(k)\end{aligned} \end{split}\]

3.2.4.1. Eigenschaften der Faltung#

Der Faltungsoperator (\(\ast\)) kann wie die Multiplikation aufgefasst werden. Es gelten die folgenden mathematische Gesetze:

  • Kommutativgesetz

\[ \label{eq:FaltungKommu} x(k) \ast h(k) = h(k) \ast x(k) \]

  • Assoziativgesetz

\[ \label{eq:FaltungAssoz} ( x(k) \ast y(k)) \ast h(k) = x(k) \ast (y(k) \ast h(k)) \]

  • Distributivgesetz

\[ \label{eq:FaltungDistrib} ( x(k) + y(k)) \ast h(k) = x(k)\ast h(k) + y(k) \ast h(k) \]

3.2.4.2. grafische Faltung#

Die Berechnung des Faltungsproduktes lässt sich auch grafisch gut veranschaulichen. Dazu betrachten wir Abbildung 3.8. Die beiden zu faltenden Folgen \(x(k)\) und \(h(k)\) sind in a) gezeigt. Das Faltungsergebnis erhält man, wenn man eine der Folgen zeitlich spiegelt b), also an der y-Achse umklappt und diese Folge über das andere Signal schiebt c). Der Ausgang d) ergibt sich immer aus der Summe der sich überlappenden und miteinander multiplizierten Einzelimpulse der beiden Folgen.

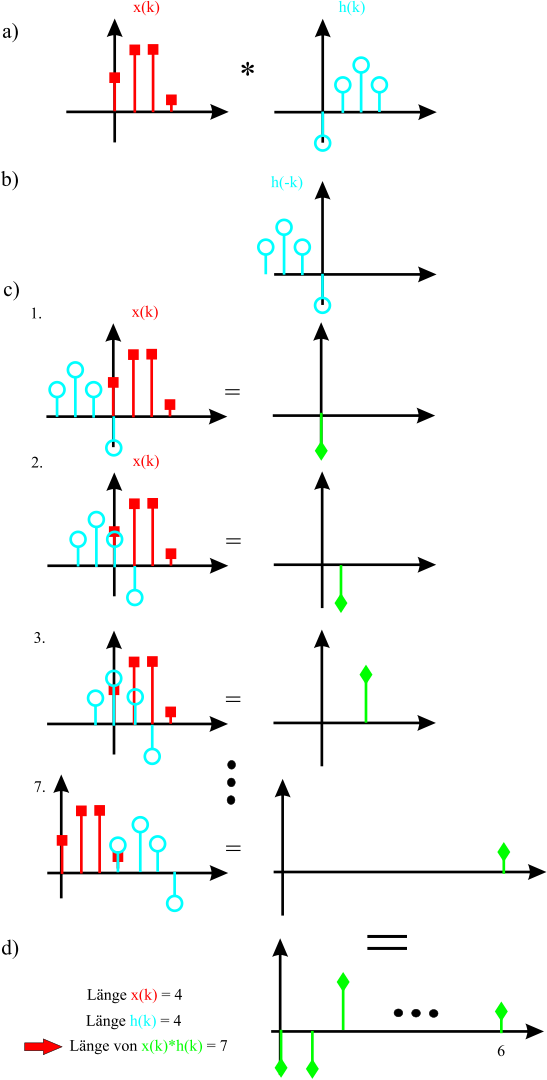
_images/FaltungserklaerungCorel.png

Fig. 3.8 Erklärung der grafischen Faltung.#

Die Länge der Ausgangsfolge ergibt sich aus der Addition der Länge der Eingangsfolge \(M\) und der Länge der Impulsantwort \(K\) zu

\[ N = M + K - 1. \]

Dies ist auch anhand der beiden grafischen Beispiele leicht zu sehen.

1

Dies könnte jederzeit durch eine Division durch \(a_0\) erreicht werden.

2

Die Impulsantwort wird hier in einer Vektorschreibweise eingeführt.