7. Übungen#

Dieser Abschnitt enthält eine Sammlung an Wiederholungsfragen und Übungsaufgaben. Die Übungen sind nach den Buchkapiteln sortiert, zum Teil ergeben sich thematische Überschneidungen. Zu jedem Kapitel gibt es Übungen zur Wiederholung des Stoffes und einfache Rechenaufgaben, gefolgt von Aufgaben (auf Klausurniveau) und Programmieraufgaben. Einige Programmieraufgaben sind noch für Matlab formuliert, eine Anpassung für Python folgt in Zukunft.

7.1. Signale#

7.1.1. Wiederholung des Stoffes und einfache Rechenaufgaben#

Klassifizieren Sie folgende Signale anhand der in Kapitel 2 angegeben Merkmale:
- $si(t)$
- Das digitale (SP-DIF) und analoge Signal eines CD-Players
- Ein DVD-Film
- Vielleicht ihr Beispiel
Was ist die Grundvoraussetzung für eine erfolgreiche Digitalisierung?
Warum verliert man Informationen bei der Digitalisierung?
Warum lassen sich Funktionen mit Knickstellen (Bsp: Dreieck) nicht wirklich digitalisieren?
Welches ist die höchste Harmonische einer aliasingfreien Dreieckschwingung mit der Grundfrequenz $f = 440$
Hz, bei einer Abtastrate von $f_s = 48000$ Hz?
Zeigen Sie, dass $si$(0) = 1 ist!
Zeichnen Sie $x(k) = 2\delta(k + 2) - 0.5\delta(k - 1) + 3\delta(k - 2)$ .

7.1.2. Aufgaben (Auf Klausurniveau)#

Wie hoch ist die Leistung eines mittelwertfreien Dreieckssignals mit der Amplitude A?

7.1.3. Programmieraufgaben#

Programmieren Sie eine Funktion, die einen Mid-Tread Quantisierer mit einer Auflösung von 4 Bit
realisiert. Versuchen Sie so allgemein zu programmieren, dass Sie jederzeit die Auflösung ändern können.
Programmieren Sie einen Rechtecksignal-Generator mit und ohne Aliasing.
Erzeugen Sie eine Funktion die eine Delta-Impulsfolge mit vordefinierter Länge (Angabe in Sekunden und $f_s$) zurückgibt.

7.2. Systeme#

7.2.1. Wiederholung des Stoffes und einfache Rechenaufgaben#

Ist ein Quantisierer ein lineares System, da ja von linearer Quantisierung gesprochen wird? Begründen Sie ihre Antwort.
Sind die folgenden Systeme zeitinvariant, kausal und linear? Begründen Sie ihre Antwort.
- $y(k) = x(k) + 2d$ mit $d\neq 0$
- $y(k) = a_1 x(k-2) + a_2 x(k-3)$
- $y(k) = k x(k-1) + x(k-2)$
- $y(k) = log_{10}( x(k-2)) + 3 x(k-1)$
Falten Sie die folgenden vier Signale jeweils grafisch mit sich selbst und mit allen anderen Signalen.

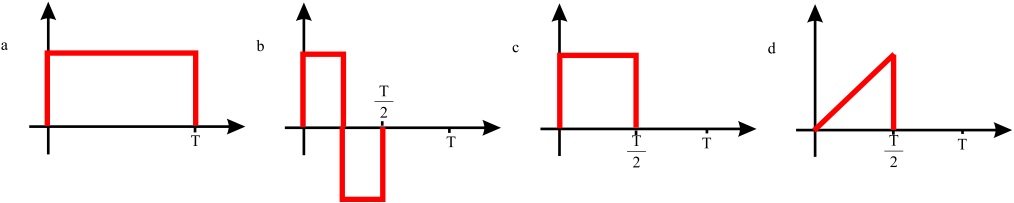
Fig. 7.1 Testsignale zum Üben der grafischen Faltung#
Zeigen Sie, dass das Kommutativgesetz der Faltung allgemein gilt.

7.2.2. Aufgaben (Einige auf Klausurniveau)#

Geben sie die Impulsantwort für die folgenden Differenzengleichungen an. Brechen Sie bei unendlichen Folgen nach $k=10$ ab. Nehmen sie an, dass sich das System zum Zeitpunkt $k=0$ in Ruhe befand.
- $y(k) = 0.5x(k-1)+ 0.3x(k-2)+ 0.4x(k-3) - 0.4 x(k-4)$
- $y(k) = y(k-1)+0.5x(k)$
- $y(k) = 0.25 x(k-1)+0.75 y(k-1) - 0.75y(k-3)$
Gegeben ist das System $0 = \frac{1}{k} x(k) + 2x(k-2) - 0.5y(k-1)$. Begründen Sie Linearität und Zeit-Invarianz bitte mathematisch formal!

7.2.3. Programmieraufgaben#

Testen Sie folgende Systeme auf Zeitinvarianz und Linearität durch Rauschfolgen als Eingangssignale. Haben Sie im Hinterkopf, dass Sie mit Zahlentests nichts beweisen können. Eine Aussage ist nur für Nicht-Linearität und Zeitvarianz möglich. Dies ergibt sich, wenn der Test fehl schlägt, da ein Gegenbeispiel ausreicht um Linearität oder Zeitinvarianz auszuschließen.
- $y(k) = x(k) + y(k-1)$
- $y(k) = 3 y(k-1) + 2 x(k-1) + x(k)$
- $y(k) = k x(k-1) + x(k-2)$
- $y(k) = log_{10} x(k-2) + 3 y(k-1)$
Erzeugen Sie eine Funktion die eine Delta-Impulsfolge mit vordefinierter Länge zurück gibt.
Nutzen Sie diese Funktion, um ihre Ergebnisse aus Abschnitt 7.2.2 Aufgabe 1 zu überprüfen.
Erzeugen Sie kurze Sequenzen mit $T = 12$ Werten um die oben gezeigten Signale zu approximieren. Überprüfen Sie Ihre Ergebnisse mit dem conv-Befehl.

7.3. z-Transformation#

7.3.1. Wiederholung des Stoffes und einfache Rechenaufgaben#

Welche Bedingungen müssen gelten, damit ein LTI-System stabil ist?
Welche Beschreibungen eines LTI-Systems kennen Sie?
Warum ist die Angabe der z-Transformationsfunktion nicht ausreichend?
Testen Sie die folgenden LTI-Systeme auf Stabilität:
- $y(k) = -2y(k - 1) + 1.5x(k) - 2x(k - 1)$
- $y(k) = 2.5x(k - 1) + 1.83y(k - 1) - 0.99y(k - 2)$
- $y(k) = 0.3x(k) + 0.7x(k - 1) + 1.9812y(k - 1) - 1.0201y(k - 2)$
Zeigen Sie, dass die Ungleichung (4.30) gilt.

7.3.2. Aufgaben (Auf Klausurniveau)#

Zeigen Sie, dass die z-Transformation eine lineare Transformation ist, indem Sie den Linearitätstest durchführen.
Welchen Wert hat das folgende System nach 50 Schritten. Geben Sie die direkte Berechnungsmethode an. Ist das System BIBO-stabil?
$y(k) = \sqrt(2) y(k-1) - y(k-2) + 0.5 \delta(k)$
Sind die folgenden Systeme kausal, stabil, linear und zeitinvariant? Begründen Sie ihre Antwort (auch wenn Sie keine Aussage machen können) mathematisch oder textuell (16)!
- $y(k) = 0.5 y(k-1) - 0.3 y(k-2) k + 0.4 x(k) - 0.5x(k-1)x(k-2)$
- $y(k+1) = 1.1 y(k-1) - 0.5 x(k+1) + 0.3 x(k) - 0.5x(k-1)$
- $y(k+1) = 2x(2k-k) - y(k+1) + 4 x(k-2) + 1.8 y(k-1)$
- $y(k) = 0.3 x(k) + 0.6x(k-1) - 0.7 x(k-2)y(k-2) + x(2k-2)$
Ist das folgende Systeme kausal, stabil, linear und zeitinvariant? Begründen Sie ihre Antwort mathematisch oder textuell! Falls Sie keine Aussage treffen können, begründen Sie auch dies!
$y(k+1) - 2y(k+2) + \alpha x(k+2) + x(k+1) = 1.99 y(k)$
Nehmen Sie an $\alpha = 2$ (8 Punkte). Für welche Bereiche von $\alpha$ (rein reell) ist das System stabil (Begründung)? (2 Punkte)
Sind die beiden folgenden Systeme kausal, stabil, linear und zeitinvariant? Begründen Sie ihre Antwort mathematisch oder textuell! Falls Sie keine Aussage treffen können, begründen Sie auch dies!
- $y(k) + \beta^2 y(k-2) + x(k-2) = 2 x(k) - 2x(k-2) - 1.9y(k-1)$.
  Zur Beantwortung der Frage nehmen Sie an $\beta = \sqrt{0.5}$ (8 Punkte).
  Für welche Bereiche von $\beta$ ist das System stabil bzw. instabil (4 Punkte).
- $2y(k) - 3.7x(-k-2)k -0.3y(k-3) = 10x(k-10)$. (8 Punkte)
Kennzeichnen Sie die Teile der folgenden Gleichungen, die darauf hinweisen, dass kein LTI-System vorliegt! (NL - nichtlinear; ZV - zeitvariant)
- $ 2 y(2k-k)x(k-1) - e^{3}x(k)k 0 x(k^{2}) = -\frac{y(k-1)}{\beta} + 2x(k)y(k-2) $
  Nehmen Sie an $\beta > 0$ ist eine reelle Zahl.
- $ 2 x(k-2)x(k-1) \frac{1}{2k} - 2y(k+1) + (3k - (1+3k))x(k) = \sqrt{log(2)}y(k) - x(k+1)$
- $ (k - (1+k)) x(k+1) - 2y(k-1) -2 = y(k) - x(2k+1) + sin(0.5)x(k) $
- $ |x(k)| + \frac{x(2k-k)}{\beta} + 1 = y(2k-1) -2y(k) - e^{5}x(k)$
  Nehmen Sie an $\beta > 0$ ist eine reelle Zahl.
- $ e^{2}y(k) -2x(k+2) + 3x(k-1)x(k-1) - \frac{2}{k}y(k+2) = (4k -(1+4k))x(k) + 4$

7.3.3. Programmieraufgaben#

Lösen Sie die Aufgabe 2 aus Abschnitt 7.3.2 durch den Aufbau des Systems und Iteration.
Programmieren Sie eine Funktion, die einen Pol-Nullstellenplan zeichnet und zusätzlich im Titel den $b_0$-Koeffizienten ausgibt. Nutzen Sie als Anhaltspunkt die zplane Funktion von Matlab. Hinweis: Sie benötigen den axis Befehl um eine quadratische Grafik aufzubauen (siehe help). Sie sollten die mpoles Funktion nutzen, um Mehrfach Null- bzw. Polstellen herauszufinden.
Schreiben Sie eine Funktion, die es ermöglicht Systeme durch eine grafische Eingabe mit der Maus zu definieren. Zeichnen Sie dazu den Einheitskreis in eine figure. Hinweis: Sie benötigen den ginput Befehl für die Maus-Eingabe und axis, um eine quadratische Grafik zu erzeugen.

7.4. Spektren#

7.4.1. Wiederholung des Stoffes und einfache Rechenaufgaben#

Bei einer Abtastrate von 44100 Hz und einer DFT Auflösung von $1024$ soll ein Sinus erzeugt werden, der keinerlei Leakage-Effekt zur Folge hat. Welche Frequenzen sind mögliche Kandidaten.
Wozu werden Fensterfunktionen benötigt?
Nach welchem Prinzip kann die Rechenleistung der DFT reduziert werden?
Welchen Einfluss haben Pole auf das Übertragungsverhalten und welchen Einfluss Nullstellen?
Wodurch entsteht ein Allpass-System?
Erklären Sie, die Folgen des Übergangs von der DTFT zur DFT!
Um zu zeigen, dass nicht-lineare Systeme neue Frequenzen erzeugen, sollten Sie das System $y(k) = x^2(k)$ mit der Exponentialschwingung anregen und sich das Ergebnis anschauen
Ein mit 200Hz abgetastetes reelles Signal wird mit einer 8 Punkte DFT spektral analysiert. Welche Frequenzbereiche sind in den 8 Spektralwerten enthalten? Welche dieser Werte (Indize) haben den gleichen Betrag?
Zeichnen Sie qualitativ die Betragsübertragungsfunktion für die folgenden durch einen Pol-Nullstellenplan gegebenen Systeme:

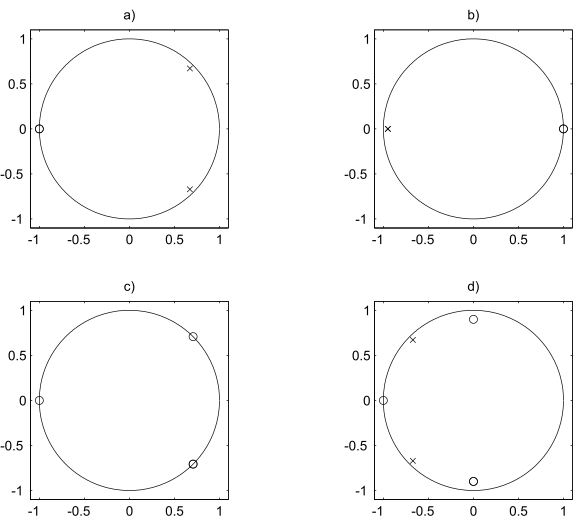
Fig. 7.2 Verschiedene Systeme und ihre Pol-/ Nullstellenverteilung#
Berechnen Sie das Spektrum einer Cosinus-Schwingung der Frequenz 2000 Hz bei einer Abtastrate von 6000 Hz, wenn Sie eine 6 Punkte DFT verwenden.

7.4.2. Aufgaben (Auf Klausurniveau)#

Welche Pol-Nullstellenlage würde die folgende Betragsübertragungsfunktion mit dazugehöriger Phase bei einem reellwertigen, stabilen System zur Folge haben ($f_s = 8000$ Hz)? (Genauere qualitative Skizze (Grosser Kreis bitte!) und kurze stichpunktartige Begründung für die relevanten Punkte)(8)
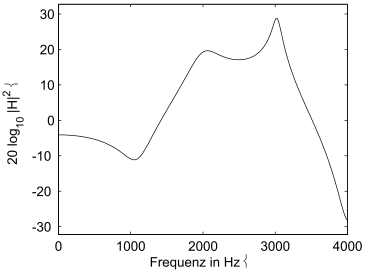
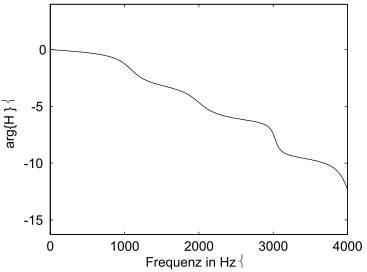
Berechnen Sie die Übertragungsfunktion zur Impulsantwort $h(k) = [1\;\; 0\;\; 1]$
Berechnen Sie die Übertragungsfunktion zu dem folgenden Filter: $y(k) = x(k) - \alpha y(k-1)$.
Skizzieren Sie die Funktion für $\alpha = 0.9$ und $\alpha = -0.9$
Ordnen Sie die folgenden Pol-Nullstellenpläne (a-d) den verschiedenen Übertragungsfunktionen (1-8) zu (2 Punkte für jede richtige Zuordnung, -1 Punkt für jede falsche).
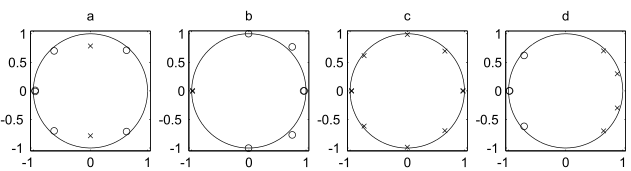
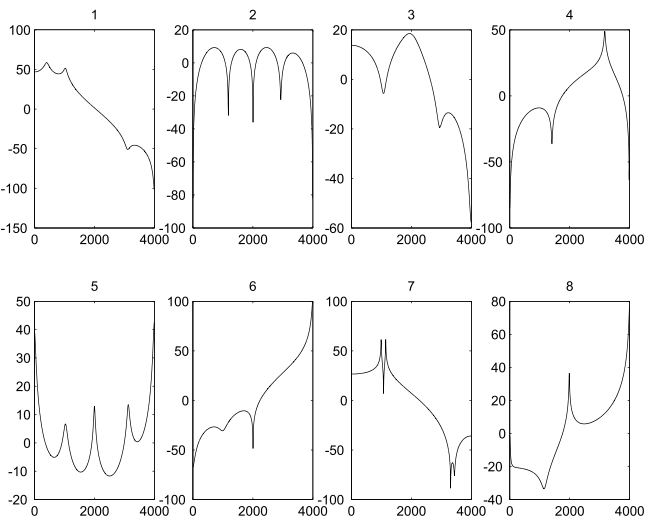
Berechnen Sie die Verstärkung des folgenden Systems bei 0 Hz:

\[ H(z) = \frac{-9 + 3z^{-1} + 7 z^{-2}}{1 + 1.9z^{-1} + 0.4 z^{-2}} \]

Geben Sie das Ergebnis bis zwei Stellen hinterm Komma genau an.
Berechnen Sie die Verstärkung des folgenden Systems bei $f_s/2$ Hz:

\[ H(z) = \frac{-0 + 10z^{-1} + 6 z^{-2}}{1 + 0.0z^{-1} + 0.7 z^{-2}} \]

Geben Sie das Ergebnis bis zwei Stellen hinterm Komma genau an.
Gegeben sind der folgende Betrag und Phase:

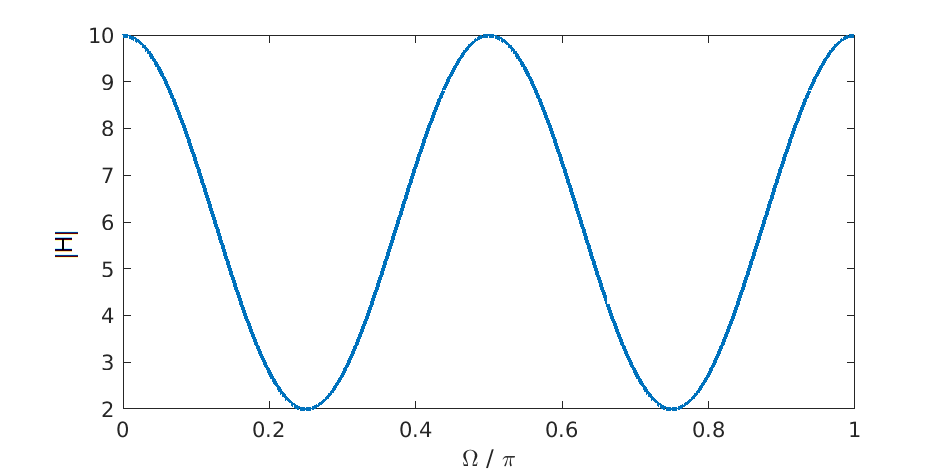
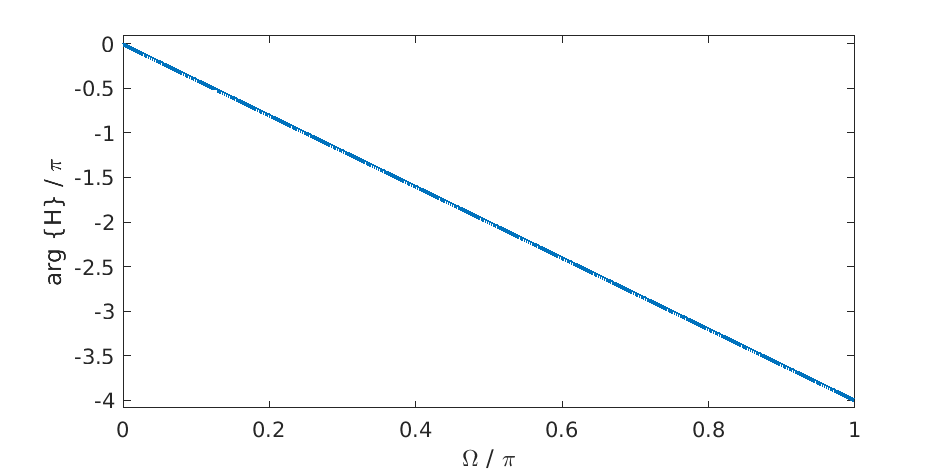
Die Zeichnung des Betrags wurde durch

$ om = 0:0.01:pi; $\ $ Habs = B+2*A.*cos((N+1)*om); $\ $ h = plot(om/pi,(abs(Habs)),’b’); $\

implementiert:

a) Zeichnen Sie die dazugehörige Impulsantwort $h(k)$ allgemein! b) Berechnen Sie dazu folgende Zwischenlösungen: Analytische Beschreibung der Impulsantwort $h(k)$ , die Systemfunktion $H(z)$ und die Übertragungsfunktion $H(e^{j\Omega})$. c) Bestimmen Sie $A$, $B$, und $N$ für das gegebene Beispiel (Mini Begründung, wie Sie auf die Lösung kommen)! (Dies ist möglich ohne eine der anderen Aufgaben zu lösen)

ca. 16 Punkte

7.4.3. Programmieraufgaben#

Bestimmen Sie die Übertragungsfunktion der folgenden Systeme.
- $y(k) = x(k) - \alpha y(k-1)$
- $y(k) = 0.3 x(k) + 07 x(k-1) + 1.9812 y(k-1) - 1.0201 y(k-2)$

7.4.4. Transferleistung#

Bei der Berechnung des Faltungsprodukts muss bei der DFT/FFT auf die Zirkularität geachtet werden. Welche Probleme können auftreten, wenn das Ausgansspektrum nicht durch Multiplikation $Y(n) = X(n)H(n)$, sondern durch eine Division $Y(n) = X(n)/H(n)$ entsteht (sog. Deconvolutionproblem)
Welche Folge hat das Decimation in Time Prinzip der FFT für den Zusammenhang der Eingangsfolge zum berechneten Spektrum. Anders ausgedrückt, was ist notwendig, damit das Prinzip funktioniert.

7.5. Filter#

7.5.1. Wiederholung des Stoffes und einfache Rechenaufgaben#

Nennen Sie jeweils eine mögliche Anwendung (am besten aus dem Bereich der Audiotechnik, Hörtechnik, Audiologie) für die verschiedenen Grundcharakteristika der Filter und überlegen sich, wie die Entwurfsparamter aussehen könnten (Grenzfrequenz, Ordnung)
Geben Sie zu folgendem Blockschaltbild die Differenzengleichung an.

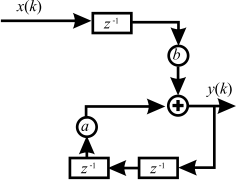
Fig. 7.3 Blockschaltbild eines Systems#
Welche Vor- und Nachteile ergeben sich durch das Overlap-Add Verfahren zur schnellen Faltung?
Zeichnen Sie zu den folgenden Systemen eine Realisierung als Blockschaltbild
- $y(k) = x(k) - \alpha y(k-1)$
- $y(k) = 0.3 x(k) + 0.7 x(k-1) + 1.9812 y(k-1) - 1.0201 y(k-2)$

7.5.2. Aufgaben (Auf Klausurniveau)#

Berechnen Sie die Übertragungsfunktion der Impulsantwort $h(k) = [-1 \;\; 1]$! Skizzieren Sie den Betrags- und Phasengang! Um was für einen Filtertyp handelt es sich (Realisierungsform und Filtercharakteristik)?
Sie sehen die folgende Impulsantwort. Um was für ein Filter handelt es sich (Realisierung und Filtercharakteristik)? Berechnen Sie die Übertragungsfunktion und skizzieren Sie den Betrags- und Phasenverlauf! Was ist besonders an diesem Filter und könnte es realisiert werden?
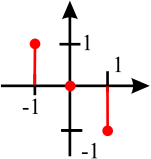
Gegeben ist das folgende System

\[ y(k) = 2x(k) + 2x(k-1) - 2x(k-3) - 2x(k-4) \]

Berechnen Sie die Übertragungsfunktion nach Betrag und Phase! Skizzieren Sie den Betrags- und Phasenverlauf zwischen 0 und $\pi$! Um was für einen Typ Filter handelt es sich? Zeichnen Sie eine möglichst effiziente Realisierung als Blockschaltbild!
Skizzieren Sie den Betragsverlauf zu dem hier vorliegenden Pol-Nullstellenplan! Welche besonderen Eigenschaften hat dieses System? Geben Sie die Übertragungsfunktion $H(z)$ als Funktion von Biquads an. Nehmen Sie an, die Radien für die Pole und Nullstellen betragen $0.9$ bzw $1.1$ und $b_0 = 1$.
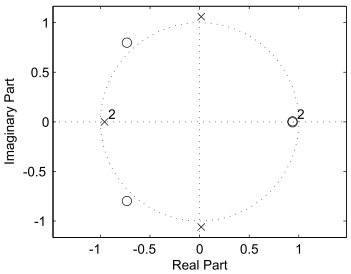
Wie lautet die Differenzengleichung und die Übertragungsfunktion des folgenden Systems nach Betrag und Phase? Zeichnen Sie den Betrags- und Phasenverlauf! Um was für eine Art Filter handelt es sich? (Typ und Realisierungsform)

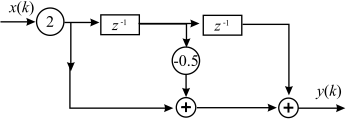
7.5.3. Programmieraufgaben#

Realisieren Sie eine Funktion, die die Koeffizienten eines mit der Fenstermethode entworfenen Tiefpasses zurückgibt. Als Übergabeparameter sollten die Grenzfrequenz, die Ordnung und das zu verwendende Fenster zur Verfügung stehen. Als Standard-Fenster soll das Rechteck-Fenster verwendet werden.
Schreiben Sie eine Funktion, die aus einem beliebigen FIR-Filter eine minimalphasige Realisierung macht, wobei die Betragsübertragungsfunktion exakt erhalten bleiben soll. Die Übergabeparameter sind nur die bisher verwendeten FIR-Koeffizienten.

7.5.4. Transferleistung#

Überlegen Sie eine weitere kanonische Struktur für SOS-Filter.
Nehmen wir an beim OLA-Verfahren wechselt die Übertragungsfunktion während der Datenvektor noch nicht vollständig bearbeitet wurde (Zeitvariantes Verhalten). Was glauben Sie ist die Folge? Können Sie sich vorstellen, wie man die auftretenden Probleme lösen kann?

Signalverarbeitung 1

Übungen

Contents